If given a 45-45-90 Triangle, then how is the area computed?
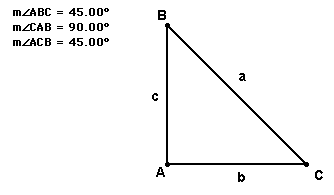
By the definition of an isoceles triangle, b=c. The hypotenuse(a) can be determined by the Pythagorean Theorem.
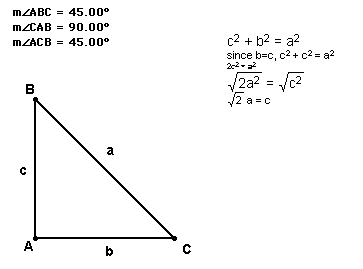
So the ratio of the sides to the hypotenuse is sqrt(2).
Objectives:
* Identify and use 45-45-90 Triangle Theorem and the 30-60-90 Triangle Theorem.
* Identify and use the formula for the area of a regular polygon.
45-45-90 Triangles:
If given a 45-45-90 Triangle, then how is the area computed?
By the definition of an isoceles triangle, b=c. The hypotenuse(a) can be determined by the Pythagorean Theorem.
So the ratio of the sides to the hypotenuse is sqrt(2).
30-60-90 Triangles:
If an altitude is drawn for an equilateral triangle, a 30-60-90 Triangle is obained.
Given the length of the hypotenuse is twice the length of the shorter leg. Find the length of all sides of a 30-60-90 Triangle.
30-60-90 Triangle Theorem: In any 30-60-90 triangle, the length of the hypotenuse is twice the length of the shorter leg, and the length of the longer leg is sqrt(3) times the length of the shorter leg.
Areas of Regular Polygons:
How would you find the area for an n-side regular polygon? You can start by dividing the shape into n congurent parts, where n is the number of sides of the polygon.
Let us start with a pentagon. Split it into parts to use a formula you already know.
Construct an altitude of a triangle to compute its area. This is called the apothem. The apothem is an altitude that extends from the center of the polygon to a side of the polygon. The apothem also is the radius of the inscribed circle of the pentagon.
To compute the area of the pentagon get the area of one triangle and multiply it by 5. To obtain a formula to find the area of a regular polygon scroll down.
Return to Instrustional Unit