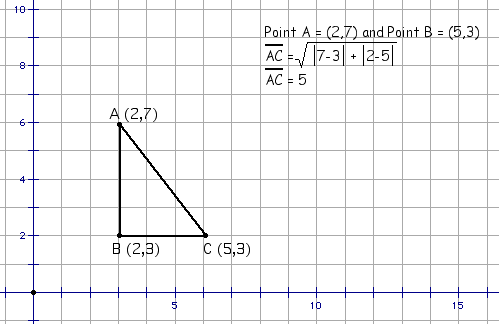
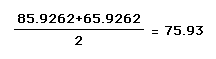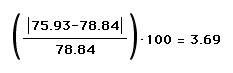The distance between two points on the same
horizontal or vertical line can be found by taking the difference
of the x or y coordinates.
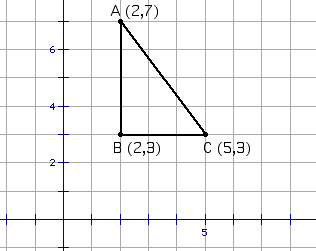
Segment AB and segment BC can found by using
the above rule. By taking the differences in the x and y coordinates
segment Ab is 4 units and segment BC is 3 units. Segment AC is
the hypotenuse of the triangle. It can be found by utilizing
the Pythagorean Theorem.
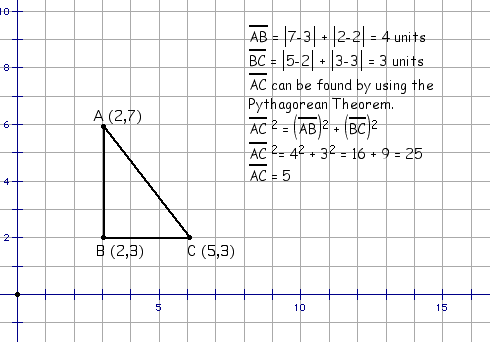
Segment AC can also be found using the same
approach used on segments AB and BC.
To prove for any triangle:
Given: Poits A and B with coordinates (x1,
y1) and (x2, y2).
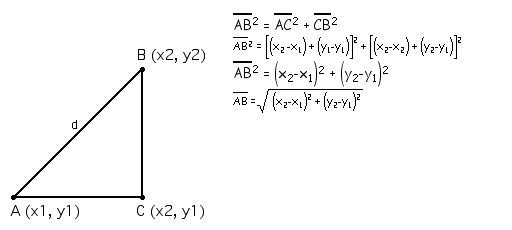
Therefore the distance formula is as follows:
In a coordinate plane the distance ,d, between
two points (x1, x2) and (y1, y2) is given by d = sqrt[(x2-x1)^2
+ (y2-y1)^2].
Quadrature is a procedure of approximating
the area of an enclosed region on a plane by using the sum of
the areas of a number of rectangles.
I. Left-Hand Rule:
* Start with a circle with radius of 5 units.
Draw rectangles with the upper left vertex of each rectangle
touching the curve.
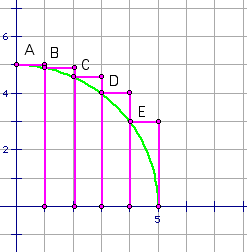
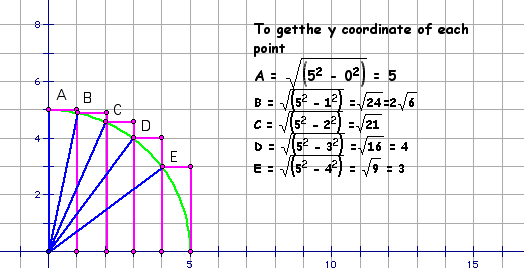
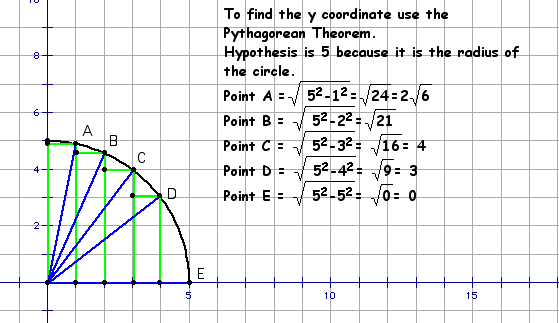
* Find the y coordinates for each vertex.
by drawing a line connecting the origin of the circle (0,0) to
each vertex. This forms a series of right triangles with thr
radius being the hypotenuse where r = 5 units. The basae of the
triangle is the x coordinate, so the third side can be found
tusing the Pytthagorean Theorem. y^2 = r^2 - x^2.
* Find the area of each rectangle. Note: the
base of each rectangle is 1.
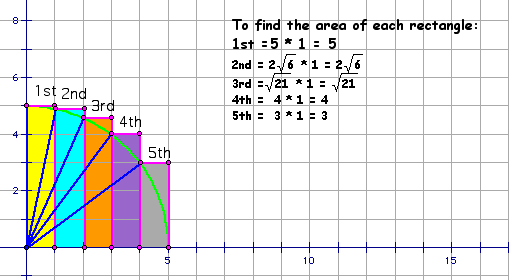
* Find the sum of the areas of the rectangles
by completing the pattern. This will give you an estimation.
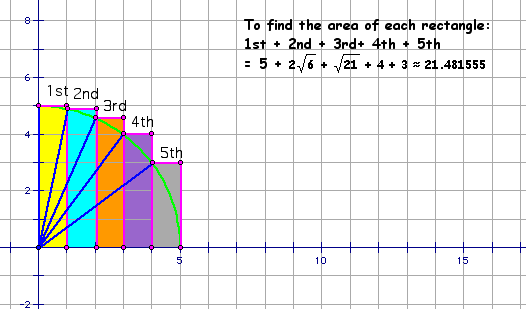
* Multiply the estimation by four to get an
estimation of the area of the original circle. 4 X 21.481555
= 85.92622. Check this by checking area of the circle with GSP.
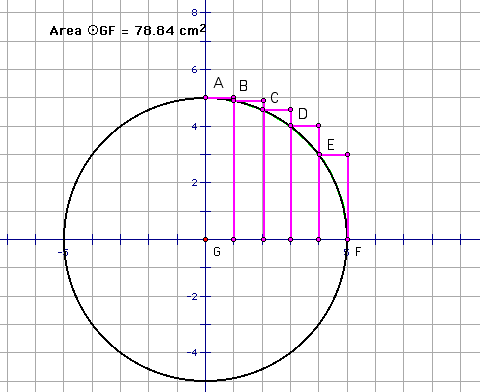
* You can see by GSP that this method overestimates
the area of the cicle and curve. The overestimation can be seen
by looking at the area of the rectangles used. The rectangles
use more area than the circle has.
* To find relative error: E = [abs(Ve - Vt)]/Vt
* 100, where Ve = estimated value, Vt = true value, and E = percent
of error. 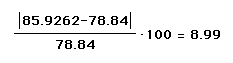 , so the Percent of error is 8.99%.
, so the Percent of error is 8.99%.
II. Right Hand Rule:
* Start with the same circle with radius 5
units as in the left hand rule. Draw the rectangles so that the
upper right vertex is touching the circle.
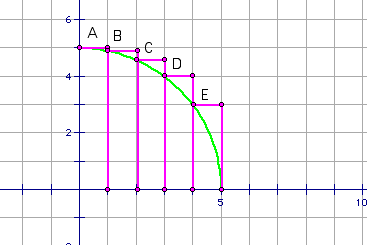
* Complete similiar method as left hand rule.
Estimate area.
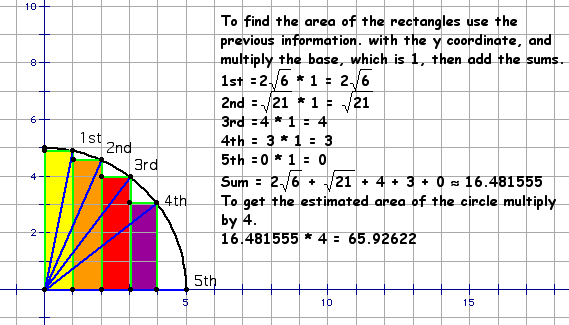
* This method understimates the area because
the estimated area obtained was 65.92622 and the true area is
78.84. Now calculate the relative error.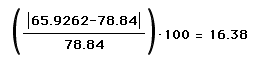 .
.
III. Average areas from parts I and II:
Take the average area of parts I and II to
get a new area. 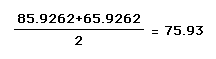
Now find the relative error for the average
of areas. 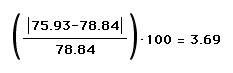
By averaging the two areas, the percent of
error decreases.



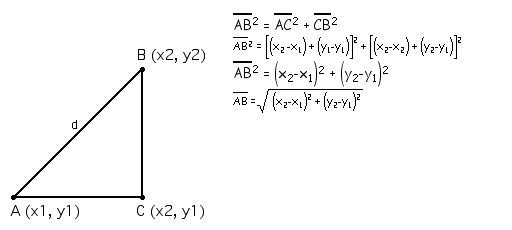





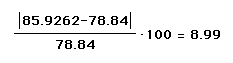 , so the Percent of error is 8.99%.
, so the Percent of error is 8.99%.


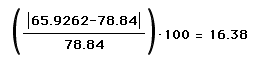 .
.