Objectives:

* Develop coordinate proofs for the Triangle Midsegment Theorem, the diagonals of a parallelogram, and a point of reflection across the line y = x.

* Use the concepts of the coordinate proofs to solve problems on the coordinate plane.

The Triangle Midsegment Theorem:

A midsegment of a triangle is parallel to a side of the triangle and has a measure equal to half of the measure of that side.

To prove this theorem, one must prove the following:

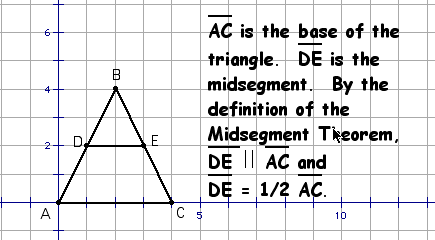
Let's look at an example:

Now let us see if works for all cases:

 

The Midsegment Theorem can be proven using other methods.

 

The Diagonals of a Parallelogram:

The diagonals of a parallelogram bisect each other.

Let's look at an example.

Now look at a general case.

It can proven also be proven in paragraph form.

 

Reflection across the line y = x:

Let's look at some examples of reflecting points across y=x to see if a pattern is seen.

(X,Y)	Reflected (X,Y)
(4,0)	(0,4)
(3,-4)	(-4,3)
(-2,0)	(0,-2)
(1,2)	(2,1)

The assumption can br made that a point (x,y) has a reflection (y,x).

Now look at the point (4,0) and its reflection (0,4):

The definition of reflection explains that the reflection of a point P, P', over a line, y=x, will result in a segment connecting P and P' at a right angle and bisecting the segment PP'.

Return to Instructional Unit