EMAT 6680 Assignment 10

Parametric Curves

Melissa Bauers Summer 2002

A parametric curve in the plane is a pair of functions (x=f(t) and y=g(t)) where the two continuous functions define an ordered pair (x,y). The two equations are usually called the parametric equations of a curve . The extent of the variation of the curve will depend on the range of t.

We will discuss the parametric equation of:

 

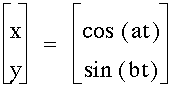
for t in the range of 0 to 6.28.

Let us break down this equation into the basic parametric equation of:

 

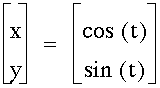
for the same range of t (0 to 6.28).

The graph looks like this.

 

 

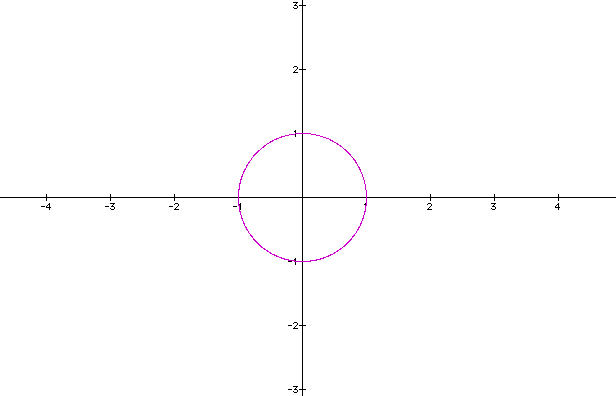
Parametric equations make it possible to graph circles. This is a circle of radius 1 that consist of two separate functions. How does adding a constant in this equation affect our graph?

We will begin with a=2 and b=2.

 

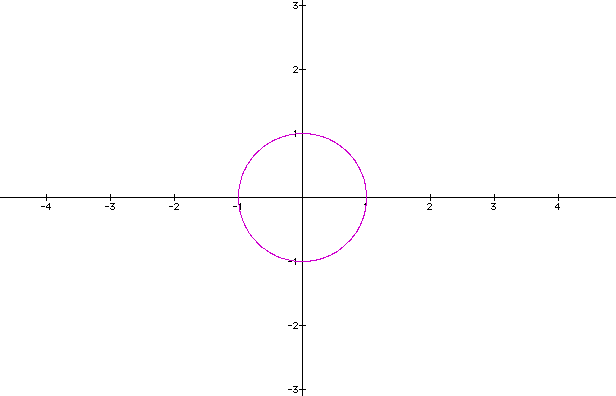
The graph looks the same.

Now let us try it for a and b being the same for the values -100 to 100. Click on the link below to see an animation of these values.

parametric #1

Now lets look at the graph if the values a and b are different. We will begin with varying one then the other. In this case we will allow a = 1 and b to vary. In the first equation, a = 1 and b = 3.

 

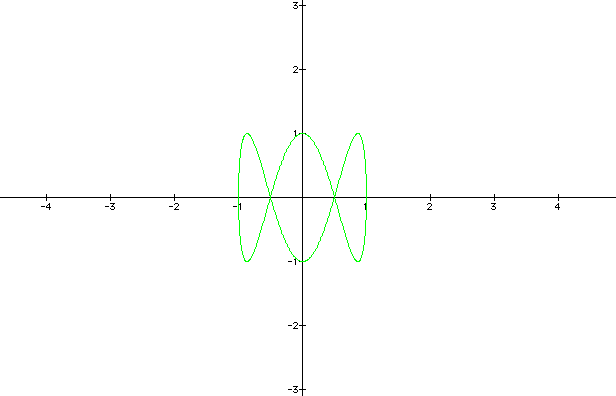
Look at b = 9.

 

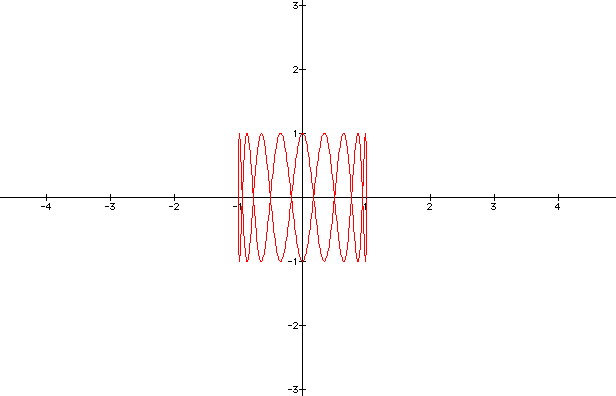
Notice that b correlated with the number of circular shapes created and that when b = -3 and -9 the graphs are the same as the positive number.

 

 

Now if b is constant at 1 and a varies.

We will begin with a = 3 and b = 1.

 

Now for b = 9.

 

 

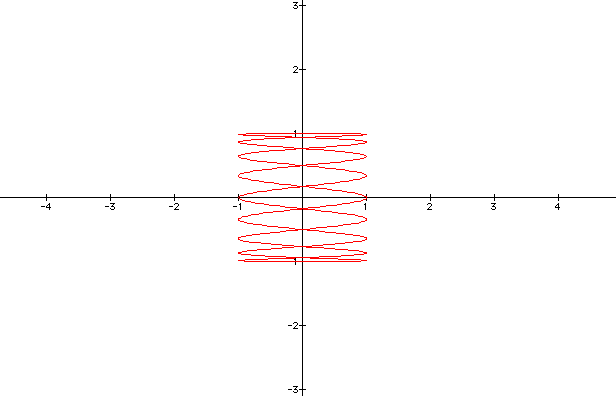
These values effect b very similar to the way it effect a, except the graph was rotated 90 degrees.

 

Now we will look at decimal values for a and b. Allow a to remain constant and b to vary.

 

 

 

 

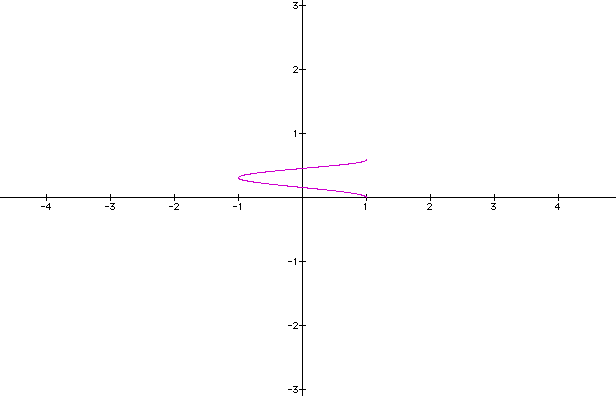
Now lets look at b = 0.1, 0.2, 0.3, and 0.5.

 

 

 

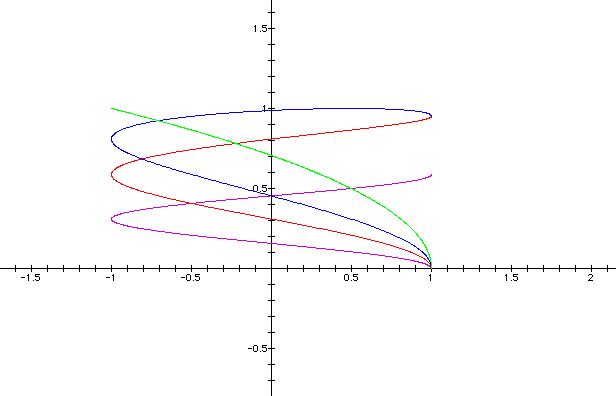
What will happen if the values are negative?

Look and see.

(b = -0.1, -0.2, -0.3, and -0.5)

 

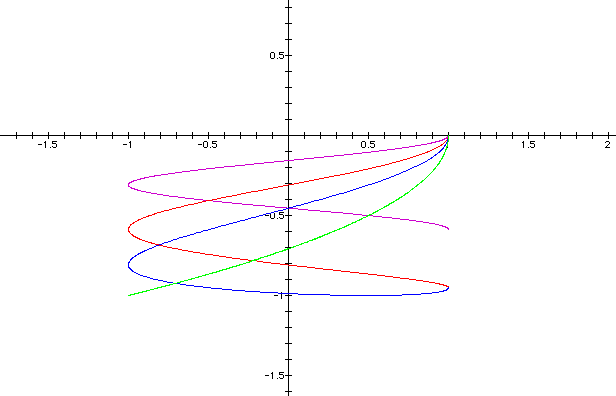
The negative values results in the reflection across the x-axis. Click on the link below to see an animation of b varying through the values -10 to 10.

Parametric When b Varies

 

 

Lets explore when a varies and b is constant (at 1).

 

 

 

 

 

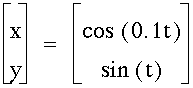
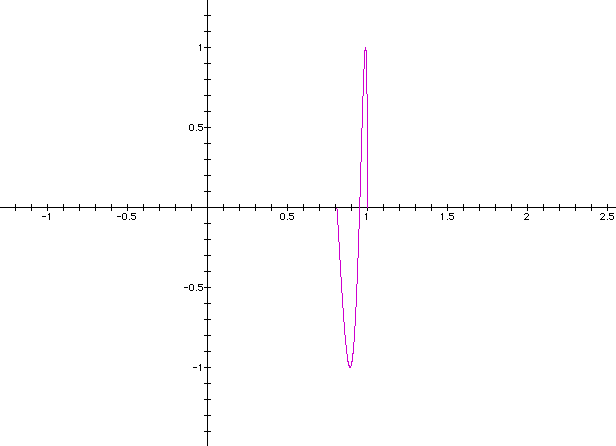
Look at the graphs for a = 0.1, 0.2, 0.3, and 0.5.

 

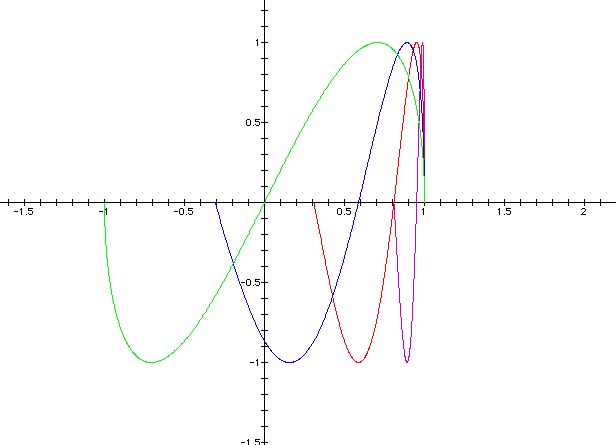
What will happen if a is a negative decimal value?

a = -0.1, -0.2, -0.3, and -0.5.

 

 

 

 

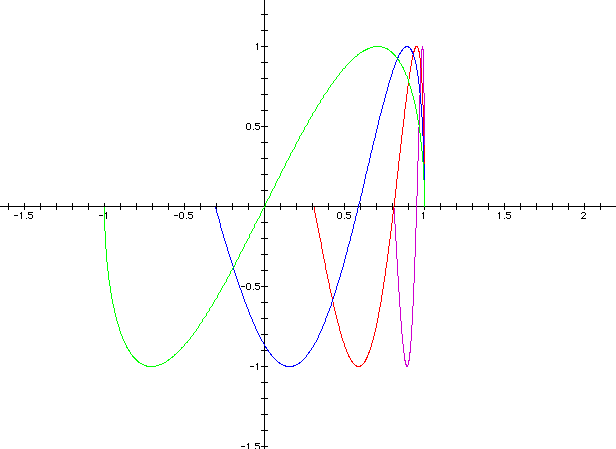
Click on the link below to see an animation when a varies form -10 to 10.

Parametric When a Varies

 

 

 

This assignment was looking at parametric equation and curves. In the equations

 

 

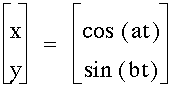
a few things were observed. When a and b were equaled, the graph resembled a circle. The graph of varying a did not depend on positive and negative values, and the values of varying b were reflection on the x-axis.