Examine the graph of y = ax².

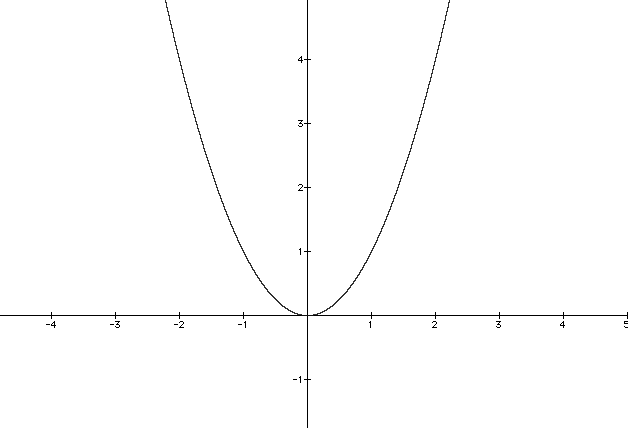
Notice the parabola passes threw (0,0). All of the values of y are positive. The graph has a relatively simple sketch.

See what happens when the value of a is 2. y = 2x²

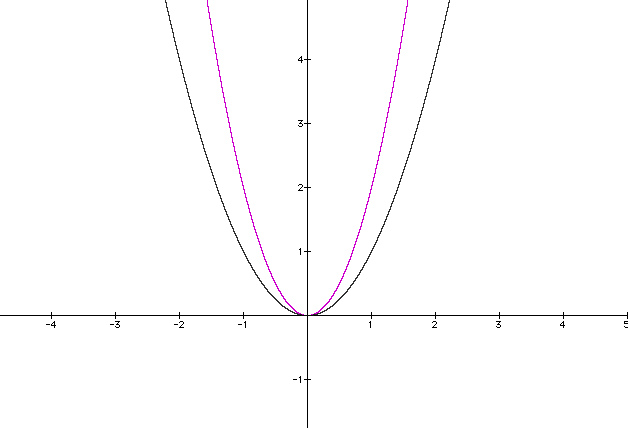
The graph is very similar to the original. What happens when a = 20? y = 20 x²

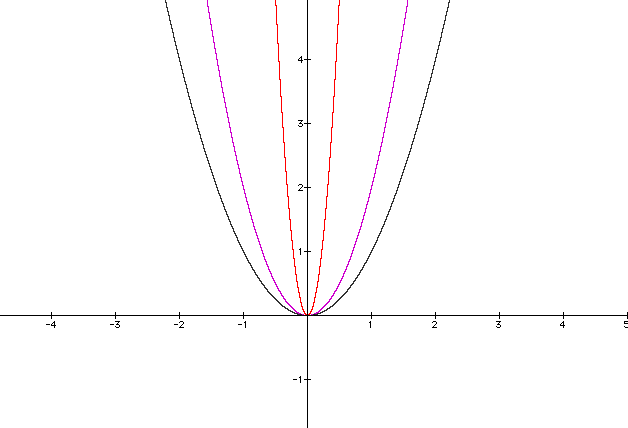
Looking at the graphs the assumption as a increases the width of the graph decreases. The graph continues to pass threw (0,0).

What needs to be done to the graph to increase the width of the graph? Let a = 1/2.

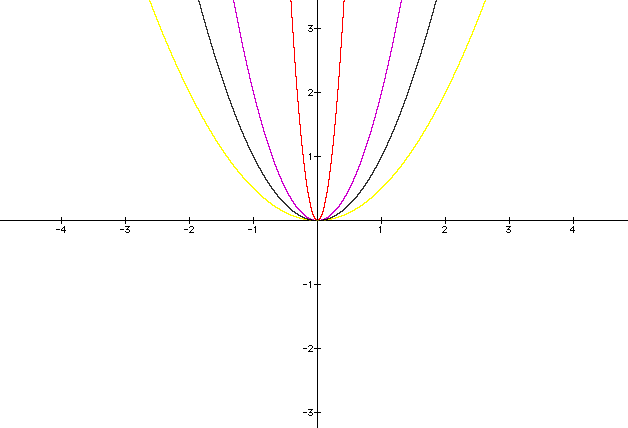
The width of the graph has increased.

Go back to the original equation and use negative numbers for a.

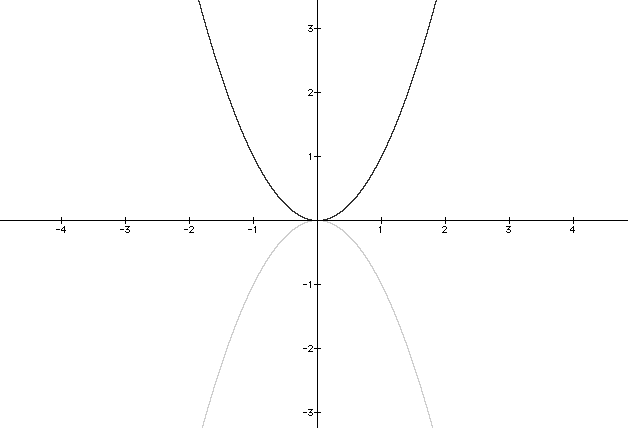
See what happens when a = -2.

y =-2x²

The graph has now has negative values for y. The point (0,0) has now become the highest point instead of the lowest point on the graph.

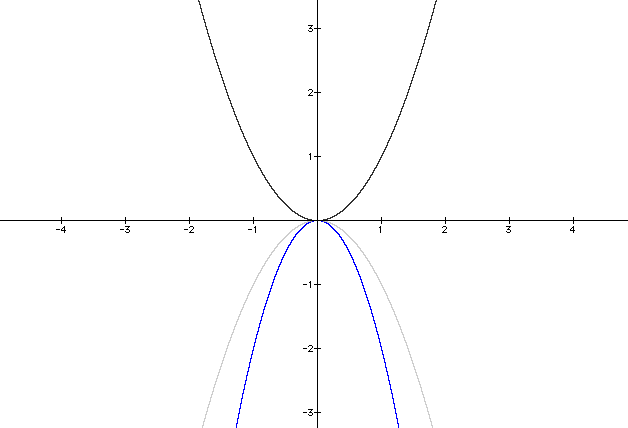
Now look at what happens when a = -20.

y = -20x²

The graph's width has decreased.

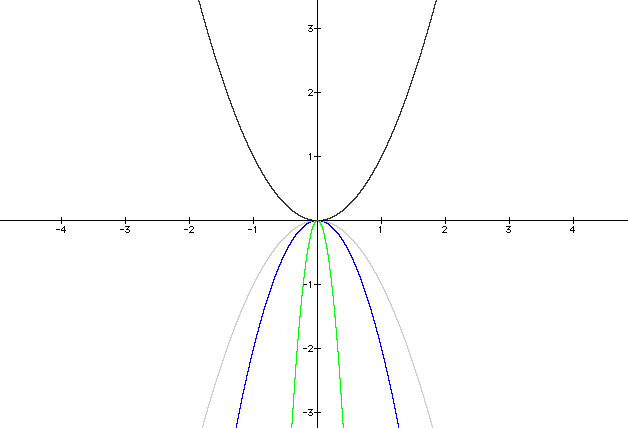
Examine what occurs if a is equaled to a negative fraction.

y = (-1/2)x²

The width of the graph increases.

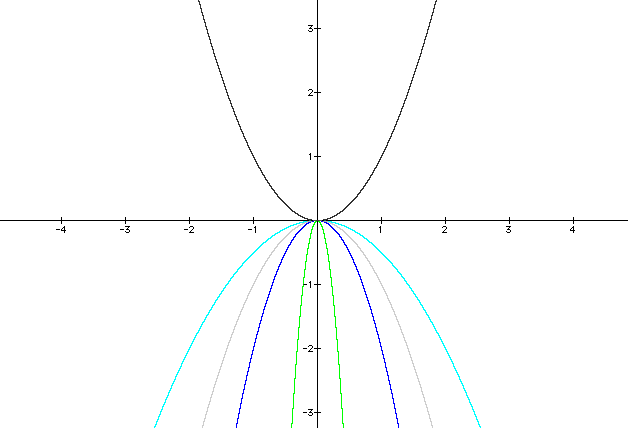
Look at all the graphs together. What assumptions can be made?

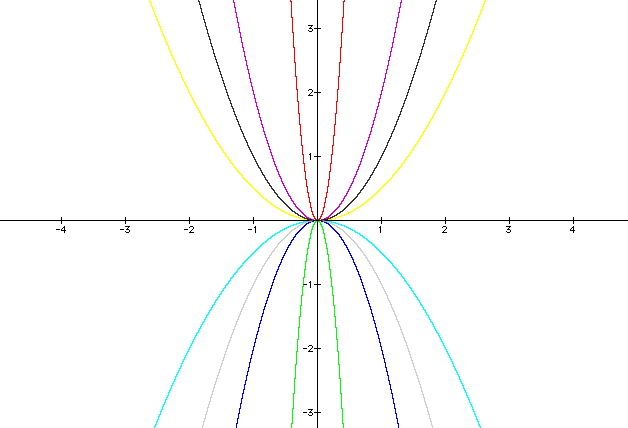
All the graphs pass threw (0,0). To change the vertex of the parabola a constant (c) must be added.

ie y = ax² + c

This equation would cause the equation to have a new vertex. The negative of a is the mirror image of a.

Return to MBauers 6680 Home Page