Proof: The three perpendicular bisectors of the sides of a triangle are

concurrent.

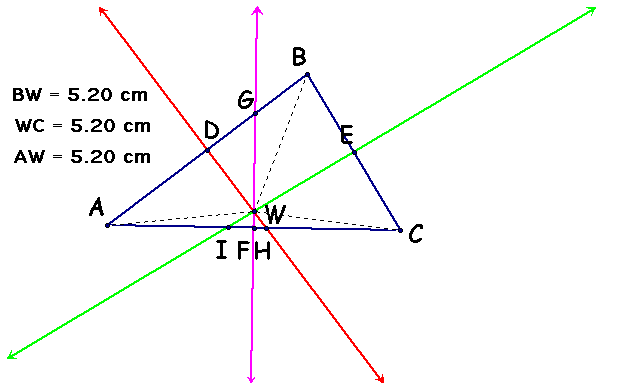
Given: Three perpendicular bisectors of D ABC

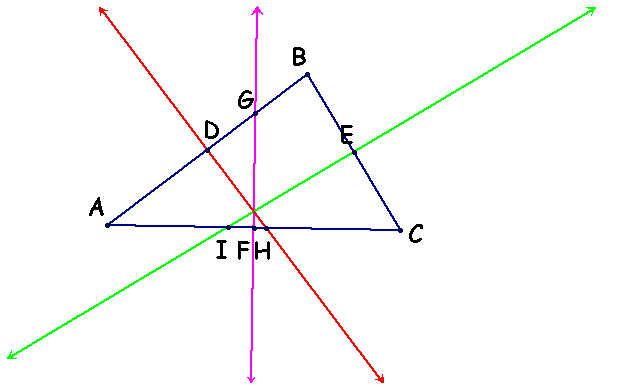
Line GF is a perpendicular bisector of line AC.

Line EI is a perpendicular bisector of line BC.

Line DH is a perpendicular bisector of line AB.

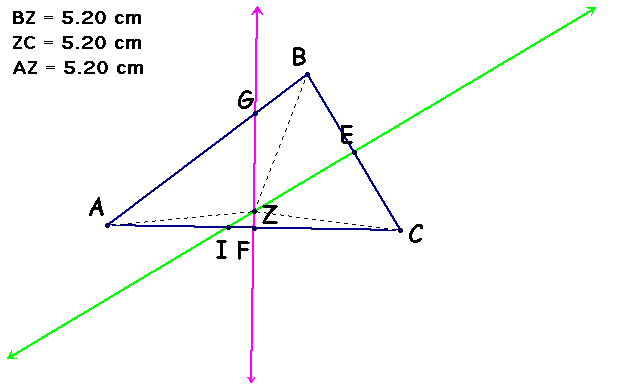
Line GF and line EI intersect at some point Z. Line GF and EI are perpendicular bisectors therefore point Z is equal distance from the vertices (by definition of a perpendicular bisector).

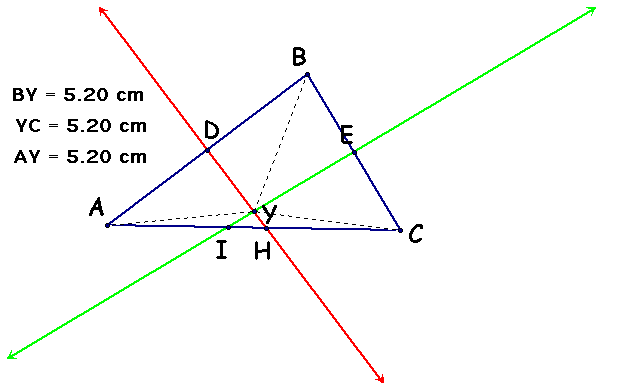
Line EI and line DH intercept at some point Y. Line EI and line DH are perpendicular bisectors therfore point Y is equal distance from the vertices of the triangle (by definition of perpendicular bisector).

Line GF and line DH intercept at some point X. Line GF and line DH are perpendicular bisectors therfore point X is equal distance from the vertices of the triangle (by definition of perpendicular bisector).

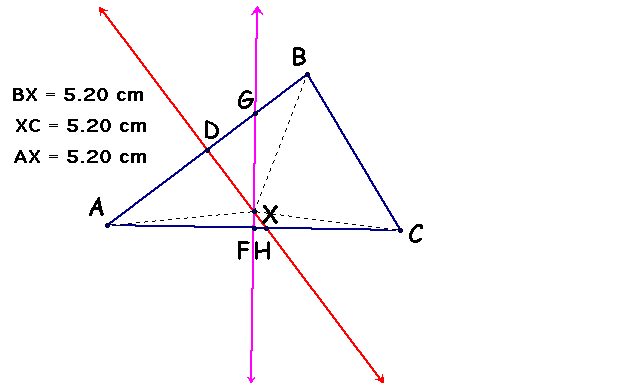
Hence points Z, Y, and X are equal distance from the vertices and are the same point. Therefore lines GF, DH, and EI are concurrent at some point W (W=X=Y=Z).

Please explore obtuse triangles using GSP. perpendicularbisectors.gsp

Return to MBauers 6680 Home Page