Given: Equilateral triangle with medians that connect to form another equilateral triangle.

Explore: a.) An isoceles triangle and its triangle of median, b.) Right triangle and its triangle of medians, c.) a median right triangle with a right angle, and d.) both the original triangle and its medians have a right angle.

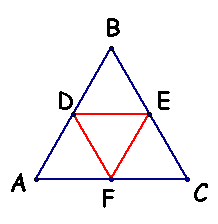
Given Triangle ABC is an equilateral triangle and its medians form an equilateral triangle.

Explore this further with GSP, Equil Assn #6.gsp

Part a.) Given Triangle ABC is an isoceles triangle (with the base being line AC), point D is the midpoint of line AB, point E is the midpoint of line BC, and F is the midpoint of line AC.

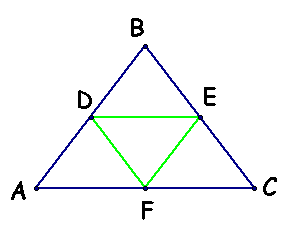
Since point D is the midpoint of line AB, then lines DF and BC are parallel to each other and DF is half the distance of line BC. Point E is the midpoint of line BC, then lines EF and AB are parallel to each other and EF is half the distance of line AB. Since lines AB and BC are equal to each other, then 1/2 DF = 1/2 EF. Therefore lines DF and EF are equal and triangle DEF is an isoceles triangle.

Explore this further using GSP, Isoc Assn #6.gsp

Part b.) Given triangle ABC is a right triangle with angle ABC=90, point D is the midpoint of line AB, point E is the midpoint of line BC, and point F is the midpoint of line AC.

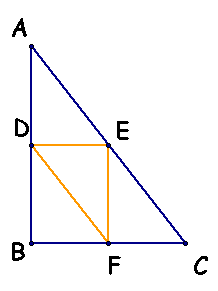
By creating auxillary lines, this figure is created to show the angle DEF = 90. By definition of supplementary angles, since angle GBH = 90 then angle DEF = 90.

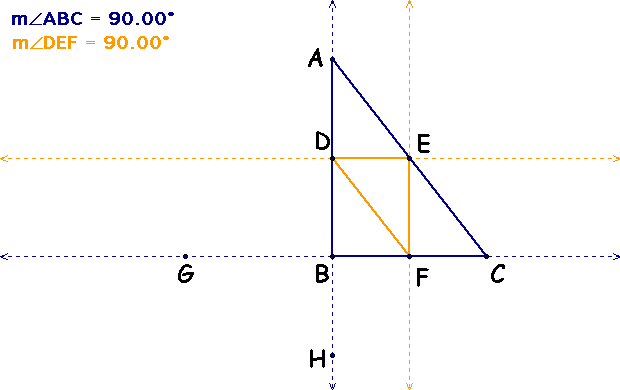
Explore further with GSP,Right Assn #6.gsp

Since a right triangle produces a right triangle with its medians, this solves parts c) and d). Both the original triangle and the median triangle must have a right angle for this proof (by definition of medians) to hold.

Return to MBauers 6680 Home Page