

If a triangle ABC has an orthocenter of H, what is the relationship of its perpendiculars to its orthocenter?
Let's observe an acute triangle ABC with orthocenter H. The feet of the altitudes are points D, E, and F. Point E lies on line AC, point F lies on line AB, and point F lies line BC.
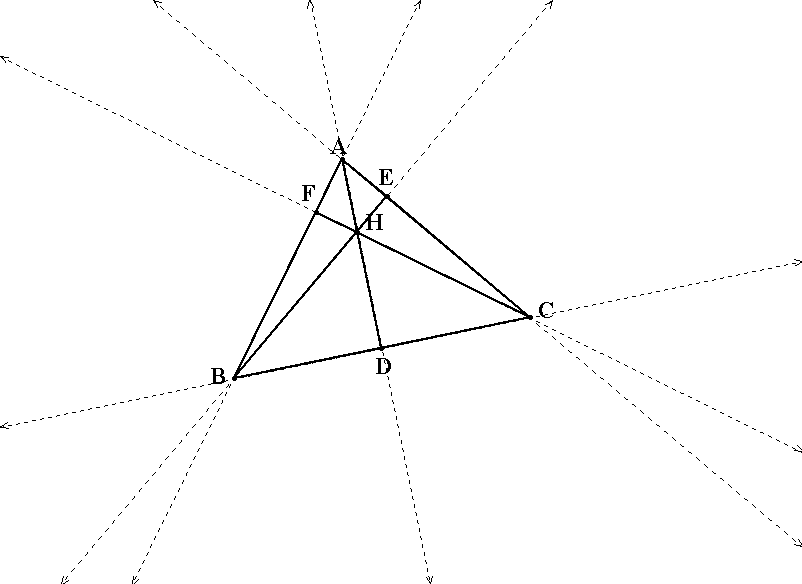
What does the expression of HD/AD + HE/BE + HF/CF equal to? What does the expression AH/AD + BH/BE + CH/CF equal to?
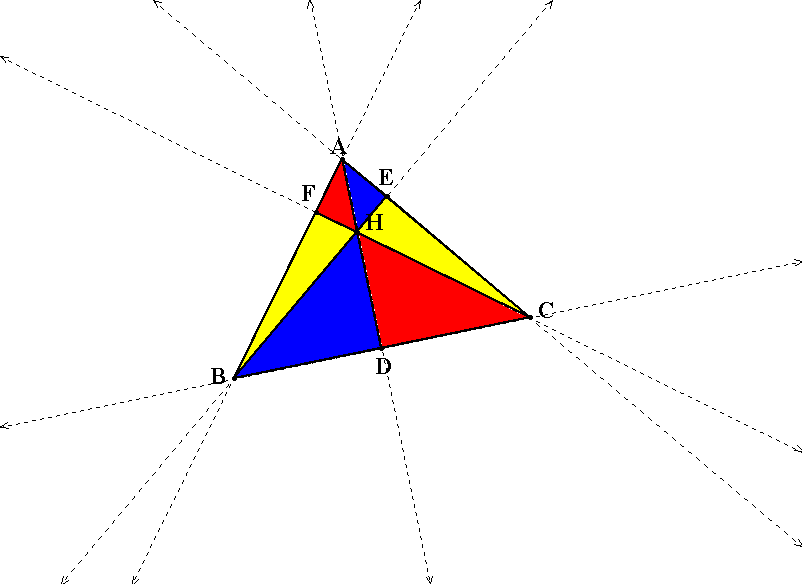
Explore triangle ABC using GSP.
Does the same relationship exist for an obtuse triangle? Do the same values hold for the expression of HD/AD + HE/BE + HF/CF and AH/AD + BH/BE + CH/CF?

Do you notice any other relationships?
Explore an obtuse triangle using GSP.