

Assingment #9 is about pedal triangles. A pedal triangle is a triangle formed by taking a geven triangle ABC and a an arbitrary point in the plane P and constructing the perpendiculars to the side of the triangle ABC from point P. The resulting intersections form the vertices of the pedal triangle. These vertices are connected and the pedal triangle to triangle ABC is triangle RST is formed. Point P is called the pedal point.
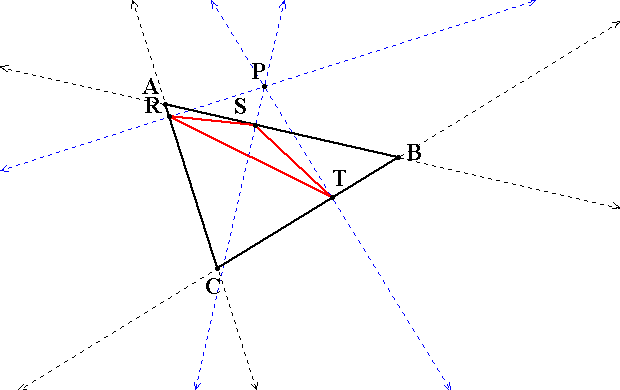
Explore Pedal Triangles on GSP by going here.
Now we will explore pedal triangles for the following cases:
1. Pedal point (P or G) is the centroid of the triangle. P is Centroid.gsp
2. P (or I) is the incenter of the triangle. Use tool table to construct new triangle.
3. P is the orthocenter of the triangle. P is Orthocenter.gsp
4. P is the circumcenter of the triangle. P is Circumcenter.gsp
5. P is the center of a nine point circle. P is Center Nine Pt Circle.gsp
6. P is on the side of the triangle. P is on Side of Triangle.gsp
7. P is on the vertices of the triangle. P is a Vertex of Triangle.gsp
Please click on the links to explore with GSP.
There is a special case involving pedal triangles where the three vertices of the triangle are colinear. The pedal triangle is a degenerate triangle. This is called the Simson Line.
Explore the Simson Line with the following GSP script. This will allow you to see the envelope of the Simson Line.
How is the Simson Line and the segment connecting P to the orthocenter related? What is the relation of intersection?
Simson Line and Orthocenter.gsp
Return to MBauers Home Page