

In this write-up, we will explore the sin function y= a sin (bx + c) and evaluate how different values of a, b, and c transform the graph.
The a value:
First, let's take a look at the graph y = sin (x) where a=1, b=1, and c=0.
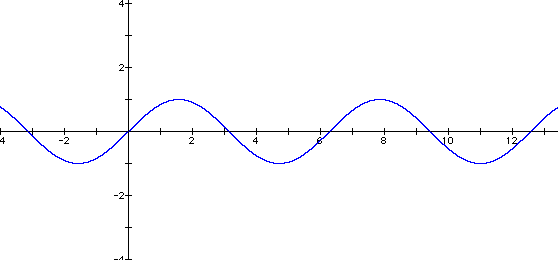
From the graph, we can tell that the range on the y-axis goes from -1 to 1. Thus, giving us an amplitude of 1. Let's look at this graph with a values of 4 and -2.
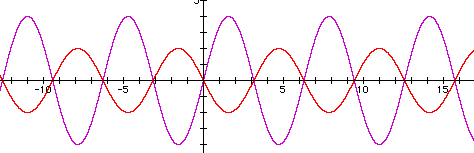
As you can see from the graphs above, both functions go through the origin. One difference between the graphs is the range on the y-axis, also called the domain. The a=4 function, y = 4 sin (x), has a domain of 4 to -4. The a = -2 function, y = -2 sin (x), has a domain of -2 to 2. Let's see if the domain continues to be a to -a by testing other a values.
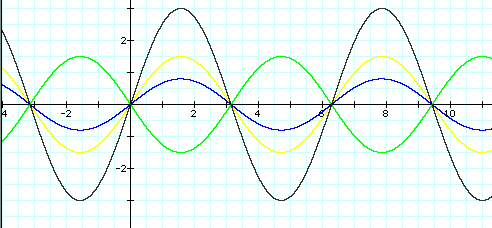
As we can see from the graph, the a value determines the domain of a to -a thus giving us an amplitude of a. By analyzing the graphs above, we see that when a=3 the amplitude is 3, when a=1.5 the amplitude is 1.5, when a=(4/5) the amplitude is 4/5, and when a=-1.5 the amplitude is 1.5. So, as a increases the amplitude increases for the positive values of a. For the case of a=0 there is no graph. Furthermore, as a increases the amplitude decreases for the negative values of a.
By looking at the yellow(a=1.5) and green(a=-1.5) functions, we can observe that the -a value reflects the graph over the x-axis.
The b value:
Now, let's explore the b value. First, let's set a=1 and c=0. Now, let's examine the graphs of b=0, b=1, b=2.
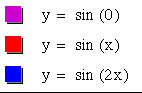
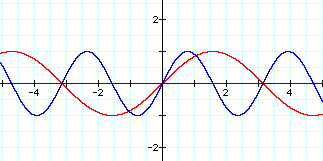
Well, it appears that our b=0 function does not have a graph. This graph is a bit misleading because sin(0)=0. So, this function would actually have a graph of (0,0), which is not seen on our graph. As we look at the b=1 function, y=sin(x) and the b=2 function, y = sin(2x), we see that the range of a cycle differs. The b=1 function has a range of about 6 and the b=2 function has a range of about 3 for a complete cycle. The term given to the cycle range is a period. From these graphs, it appears that as b values increase the period decreases. Let's test our hypothesis.
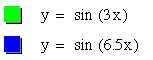
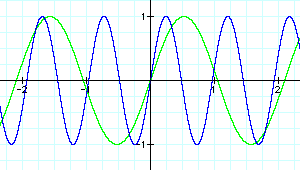
According to the graph, the function y=sin (3x) has a period of approximately 2 and the function y=sin(6.5x) has a period of approximately 1. Thus, as the b value increases, the period decreases for positive values of b. Next, let's test some negative b values.
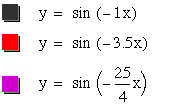
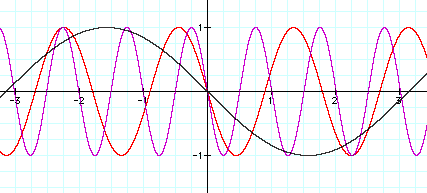
Oops, our hypothesis did not hold true for the negative values of b. By looking at the graph above, when b=(-25/4) in the purple graph, the period is around 1, when b=-3.5 in the red graph, the period is approximately 1.8, and when b=-1, in the gray graph, the period is about 6.4. So, as b increases, the period increases for negative b values.
The c value:
Finally, we will explore the c values for y=a sin (b x + c ). First, let's look at positive c values letting a=1 and b=1. We will begin with c=1, 2.5, 10/3.
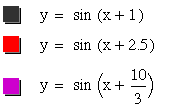
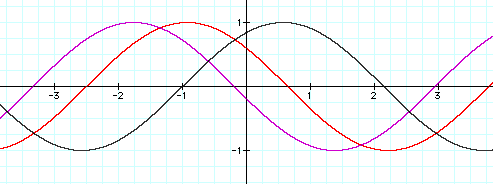
By looking at the first graph in this write-up, you can see that when c=0, the graph crosses the origin, (0,0). Now, by looking at the above functions, when c=1, the function crosses the x-axis at -1, when c=2.5 the function crosses the x-axis at -2.5, and when c=(10/3) the function crosses the x-axis at (-10/3). Therefore, c shifts the function -c units on the x-axis for positive values of c and c=0. Now, let's explore negative values of c.
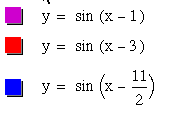
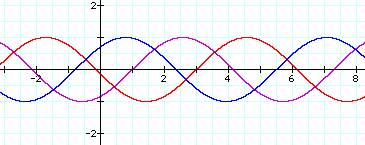
In our first function, y = sin(x-1), where c=-1, the graph shifts one unit to the right on the x-axis. In the second function, y = sin(x-3), where c=-3, the graph shifts three units to the right on the x-axis. In the third function, y = sin(x-11/2), where c=-11/2, the graph shifts 11/2 units to the right on the x-axis. The shift on the x-axis is called a phase shift. From our graphs, we can conclude that the c value shifts the graph of y = sin(x) -c units on the x-axis for all values of c.
To conclude our write-up let's look at what we found to be true about the a, b, and c, values for y = a sin(bx + c). First, we found that the a value determines the domain of a to -a thus giving us an amplitude of a. Second, we found that as the b value increases, the period decreases for positive values of b. We also found that as b increases, the period increases for negative b values. Third, we found that the c value shifts the graph of y = sin(x), -c units on the x-axis for all values of c. We call this the phase shift.