
Assignment 4
Exploring the centroid, orthocenter,
circumcenter, and incenter
By Carly Coffman
Centroid
The CENTROID (G) of a triangle
is defined as the common intersection of the three medians. A
median of a triangle is the segment from a vertex to the midpoint
of the opposite side.

We can explore the centroid
by using Geometer's Sketch Pad. Click on the link below to explore
and make observations about the centroid.
?1) Are there any cases where
the centroid is outside the triangle? If so, when did it happen?
?2) What happens to the circumcenter
when there is a degenerate triangle (when the triangle becomes
a line)?
Now, with Geometer's Sketch Pad, (GSP), create
the centroid of a triangle. Here are the steps and you can use
the link below to get back to GSP.
1) With the mouse, highlight the point tool
from the toolbox. (If you do not have a toolbox appear on your
sketch go to Display on the top toolbar and go down to Show toolbox.)
2) Create three points on your sketch by clicking
with the mouse.
3) Drag your mouse back to the toolbox and
click on the arrow (this allows you to highlight).
4) Highlight the three points
5) Go to the top toolbar, select Construct,
and go down to Segments
6) Click off the triangle to de-highlight
all objects
7) Create the midpoint of each side of the
triangle by selecting the three sides (make sure nothing else
on your sketch is selected), then go up to the toolbar, highlight
Construct and then go down to midpoint.
8) Repeat step #6, then highlight one vertex
and the opposite side's midpoint, and repeat steps #5 and #6
9) Highlight another vertex and the opposite
side's midpoint and repeat steps #5 and #6
10) Highlight the last vertex and the opposite
side's midpoint and repeat steps #5 and #6
11) Highlight the intersection of the three
lines you just created. Congratulations, you just created your own centroid!
(Do not save when exiting GSP)
Orthocenter
The ORTHOCENTER (H) of a triangle
is the common intersection of the three lines containing the altitudes.
An altitude is a perpendicular segment from a vertex to the line
of the opposite side.
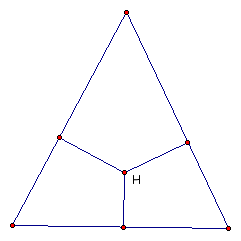
We can explore the orthocenter
by using Geometer's Sketch Pad. Click on the link below to explore
and make observations about the orthocenter.
?3) Were there any cases where
the orthocenter was outside the triangle? If so, when did it happen?
?4) What happens to the orthocenter
when there is a degenerate triangle (when the triangle becomes
a line)?
Now, with GSP, create your own orthocenter
of a triangle. Here are the steps below and you can use the link
below to get to GSP.
1) With the mouse, highlight the point tool
from the toolbox. (If you do not have a toolbox appear on your
sketch go to Display on the top toolbar and go down to Show toolbox.)
2) Create three points on your sketch by clicking
with the mouse.
3) Drag your mouse back to the toolbox and
click on the arrow (this allows you to highlight).
4) Highlight the three points
5) Go to the top toolbar, select Construct,
and go down to Segments
6) Click off the triangle to de-highlight
all objects
7) Highlight one vertex and the opposite side
only
8) Go to top toolbar, select Construct, and
go down to Perpendicular Line
9) Click off the figure to de-highlight objects
10) Highlight another vertex and opposite
side and repeat steps #8 and #9
11) Highlight the third vertex and opposite
side and repeat steps #8 and #9
12) Click on the intersection of the three
lines you just created. Congratulations, this is your orthocenter!
(Do not save when exiting GSP)
For a further exploration of the orthocenter,
click below and watch what path the orthocenter takes as you drag
one vertex along a line.
?5) What shape does the path
of the orthocenter follow?
Circumcenter
The CIRCUMCENTER (C) of a
triangle is the point in the plane equidistant from the three
vertices of the triangle. Since a point equidistant from two points
lies on the perpendicular bisector of the segment determined by
the two points, C is on the perpendicular bisector of each side
of the triangle.
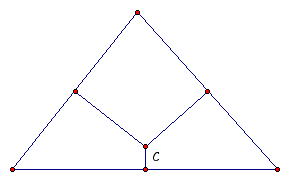
We can explore the circumcenter
by using Geometer's Sketch Pad. Click on the link below to explore
and make observations about the circumcenter.
?6) Were there any cases where
the circumcenter was outside the triangle? If so, when did it
happen?
?7) What happens to the circumcenter
when there is a degenerate triangle (when the triangle becomes
a line)?
Now, with GSP, create your own circumcenter
of a triangle. Here are the steps below and you can use the link
below to get to GSP.
1) With the mouse, highlight the point tool
from the toolbox. (If you do not have a toolbox appear on your
sketch go to Display on the top toolbar and go down to Show toolbox.)
2) Create three points on your sketch by clicking
with the mouse.
3) Drag your mouse back to the toolbox and
click on the arrow (this allows you to highlight).
4) Highlight the three points
5) Go to the top toolbar, select Construct,
and go down to Segments
6) Click off the triangle to de-highlight
all objects
7) Highlight all three sides by clicking on
them one at a time
8) Go to the top toolbar, select Construct,
and go down to Midpoints
9) Repeat step #6, then highlight one midpoint
and the side it is on
10) Go to the top toolbar, select Construct,
and Perpendicular Line
11) Repeat step #6, then highlight another
midpoint and the side it is on, and repeat step #10
12) Repeat step #6, then highlight the last
midpoint and side, and repeat step #10
13) Click on the intersection of the lines
you just created. Congratulations, you have just created a circumcenter!
(Do not save when exiting GSP)
An extension of the circumcenter is the circumcircle.
Since the vertices are equidistant from the circumcenter, we can
create a circumcircle using the circumcenter as our center and
the vertices as points on the circumcircle. This causes the circumcenter
to the each vertex to be a radius of the circumcircle. Click below
to explore.
Incenter
The INCENTER (I) of a triangle
is the point on the interior of the triangle that is equidistant
from the three sides. Since a point interior to an angle that
is equidistant from the two sides of the angle lies on the angle
bisector, then I must be on the angle bisector of each angle of
the triangle.
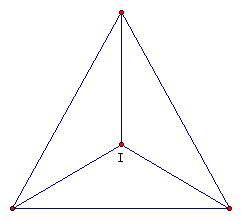
We can explore the incenter
by using Geometer's Sketch Pad. Click on the link below to explore
and make observations about the incenter.
?8) Were there any cases where
the incenter was outside the triangle? If so, when did it happen?
?9) What happens to the incenter
when there is a degenerate triangle (when the triangle becomes
a line)?
Now, with GSP, create your own incenter of
a triangle. Here are the steps below and you can use the link
below to get to GSP.
1) With the mouse, highlight the point tool
from the toolbox. (If you do not have a toolbox appear on your
sketch go to Display on the top toolbar and go down to Show toolbox.)
2) Create three points on your sketch by clicking
with the mouse.
3) Drag your mouse back to the toolbox and
click on the arrow (this allows you to highlight).
4) Highlight the three points
5) Go to the top toolbar, select Construct,
and go down to Segments
6) Click off the triangle to de-highlight
all objects
7) Now, you're going to select an angle. To
do this, you must highlight the three vertices of the triangle
with the middle one being the vertex of the angle you will bisect.
8) Go to the top toolbar, select Construct,
and go down to Angle Bisector
9) Repeat step #6, select the three vertices
again with the middle point being a different vertex, and repeat
step #8
10) Repeat step #6, select the three vertices
one last time with the middle point being the last vertex to bisect,
and repeat step #8
11) Click on the point of intersection for
these angle bisectors. Congratulations, you just created your own incenter!
(Do not save when exiting GSP)
Since the incenter is equidistant from the
three sides, the incenter also has an extension called an incircle.
Click below to see.
?10) Do you have any ideas
on how to create the incircle given the incenter? Solution





