

The problem I chose to do for this write-up is both a choice for Assignment 6 and a problem to be solved in the EMAT 6600 Problem Solving Class. The problem is also found in Mathematical Discovery by George Polya.
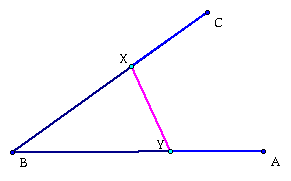
Given three points A, B, and C. Draw a line intersecting segment AC and BC where X is a point on AC and Y is a point on BC where AX=XY=YB

This picture will look something like this in the end:
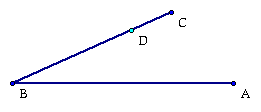
The first step is to pick some point D on segment BC. This point is a random point on BC but should not be too far from C.
Next draw a line, DE parallel to segment AB, that is the same length as DC.

Next construct point F on the segment AC so that CD=DE=EF
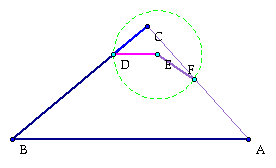
Next, connect segment CE and extend CE down to a point G on segment AB.

Now draw a line parallel to EF through A.

The intersection of this line and segment DE is H

Now when D is moved along the BC segment, the position of both H and F move accordingly. Therefore when D is at a spot on BC, such that F and A are the same point and H and E are the same point this spot for D will be called X.

At this point the circle drawn from the center point X and intersects segment AB is the other point Y that is needed.

To play more with the illustration, click here. (Must have GSP)