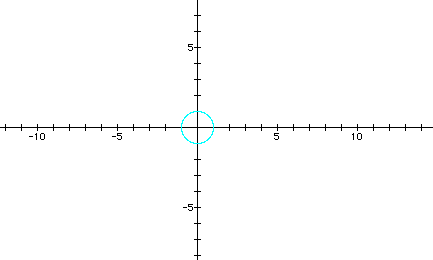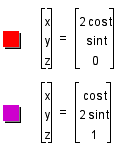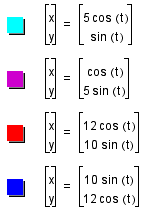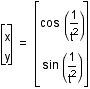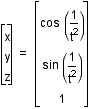We begin by examining the elementary situation of
x = sin(t)
y = cos (t)
and we allow t to vary from zero to
.
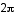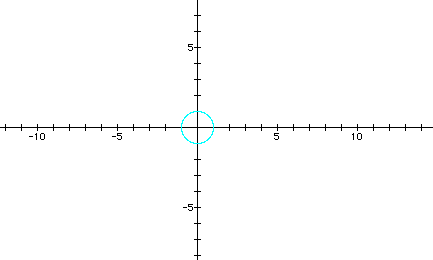The result of course is the unit circle.
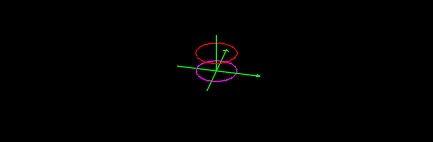
In 3 dimensions allowing
x = cos(t)
y = sin(t)
z =0
you get the perspective of the circle using a homogeneous
construction.
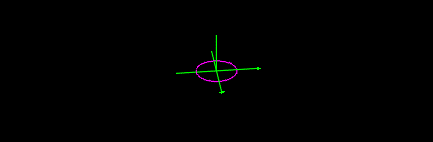
Taking things one step further you may allow z =1 .
This will produce the isomorphic circle in the
plane 1 unit above the original.
From even an elementary stand point the student should
not be spared details of concepts such as
knowing how an extra dimension may play a role in even simple
fucntions and their graphs or
merely allow a more analytical perspective.
Keeping in mind the 3 dimension perspective we continue
our exploration with the following
situations....
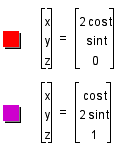
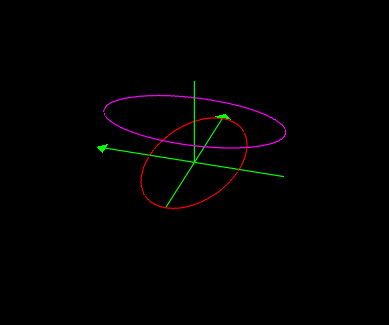To see the dynamics of the situation
click here
Next lets look at these functions as we complicate
the exploration a bit further. If we manipulate the coefficients
in front of the sin and cos expressions we add eccentricity to
the cirlce curve which is so intrinsic to the trigonometric functions.
One notices quite readily that increasing the values in front
of the expression for the x parameter creates an ellipse streched
in the x direction and intersects the x -axis at the point of
the scaled value. An analogous condition occurs for the y parameter.
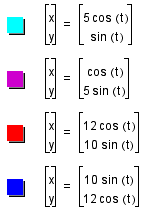
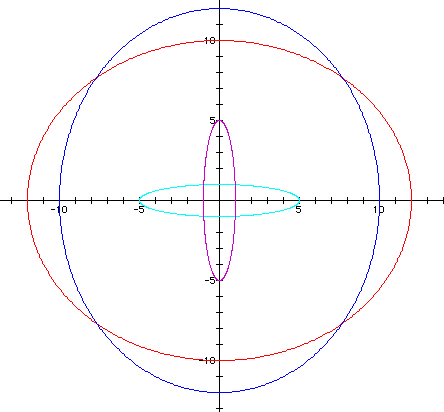
In the 3-D Plane with z= to some constant, the view
appears similar but pushed up into free-space.Using a third dimension
should lead to endless possibilites of adventure with parametric
and trigonometric functions.
As a closing are a few manipulations are offered
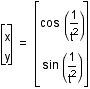
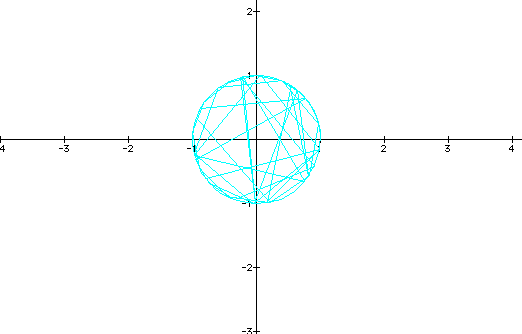
We are reminded of how the function is still a 2 dimensional
mapping and more
strongly see the features of it being a disk as well
as a complicated curve when viewing the relation
in free-space.
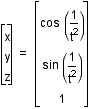
Return