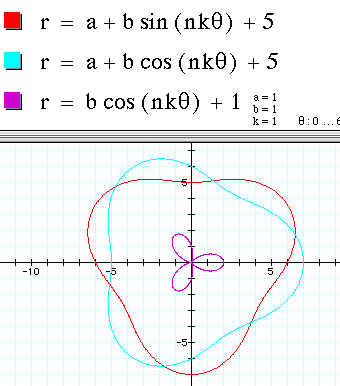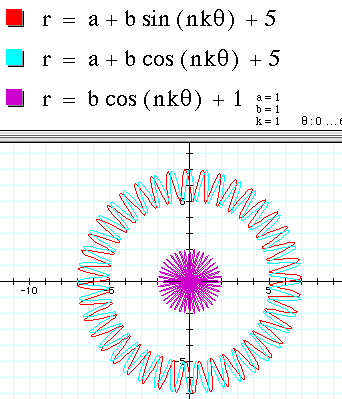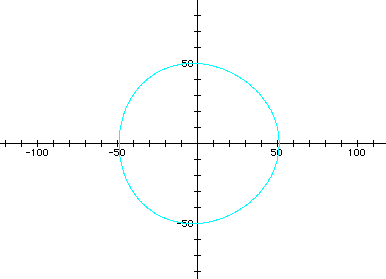We examine a very basic polar equation and pay attention
to the arrangement of the constants,
variables, and powers. Below is the graph of the following
function
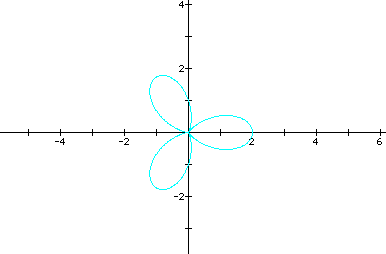
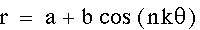This is the n leaf rose for k=n. Here, a,b, and k are
set at 1 and n =3.
Click here to see modifications
for the following equations as n varies. Notice that n makes k
change even if k is left alone at 1.
Lets examine a multitude of functions graphed together
and make some generalizations.
In the case below n=3=k . The a,b,and c are left constant,
and the constants at the end of the
equations are in place just to spread out the scenario.
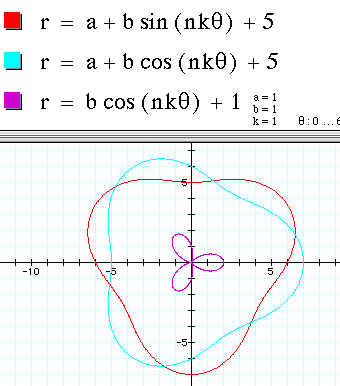To manipulate the n values click
here.
For n very large in the above scenarios you should
see something like this
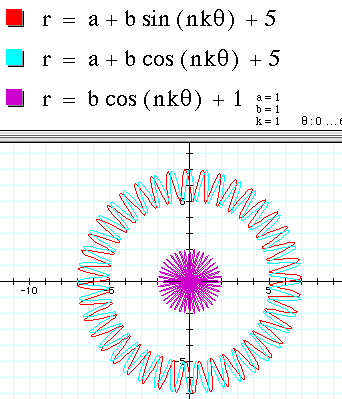
Looking back at the first example, lets explore the
intrinsic complexities of manipulating variables
and constants of even a simpler equation.
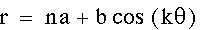As a grows large the curve ( n -leaf) blows
up, eventually minimizing the leafing characteristic
until the entire picture from the far out view becomes
circle like
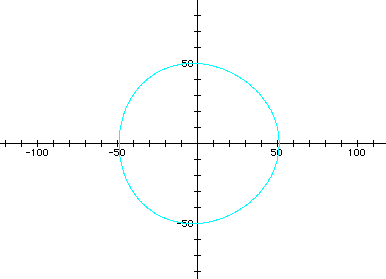To see the effect of increasing a by step click
here
Lets look at the case where the constant b is manipulated
and k=4 (the 4 leaf rose for the given
equation.
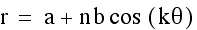
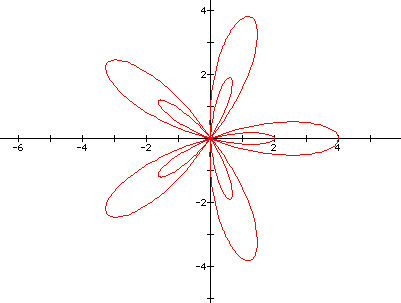
When k is odd and greater than1 the following happens
. This specific case k=5 and nb=3, as nb gets bigger( n is a scaler
here for graphing) thye picture simply blows up...
and new leaves appear inside the original leaves
When k is even (here k=6) the following happens...
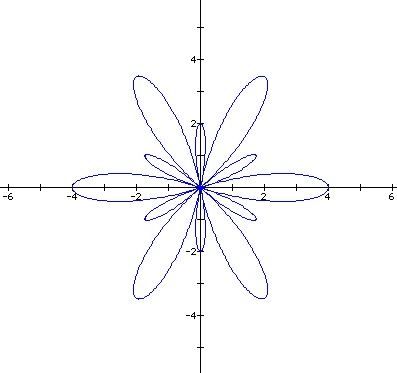new leaves grow spur outside the original, and again,
increasing b expands the entire picture.
When all three manipulations happen together, they
play their indiviudal role to a certain extent, but
still there is much to discuss. Exploration with middle of
high school students with similar
situations are endless.
Return