Drosophila are often of interest to biologists because
of their lifespan, mating habits, and the way in
which there cells are very lab friendly.
As a historical example from post World War 2 Calculus
books we refernce a study .* Growth of
a fruit fly population in a controlled experiment ,and
examine a population of Drosophila over a 23
day study using Microsoft Excel as our learning device.
To view a very close estimate to the original data
set and an initial chart click here
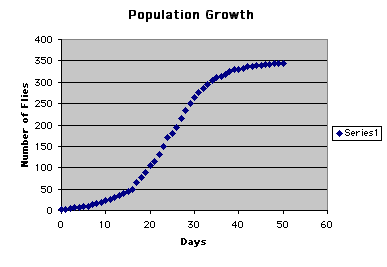
The chart for the data set shows the days (1-50) ploted
against the fly population.
We can investigate this further in elementary and intermediate
directions.
We now examine the chart of the actual population growth
ploted aginst the average growth over the entire period of the
50 day study.
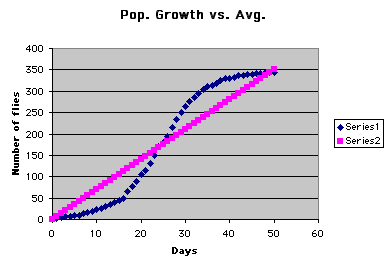As one may see the average( series 2, pink) is only
a useful estimate of the population on a few
isolated instances. The advanced student may attempt
to find a function that maps a unique point of
the number of flies for each specific day.
To view the entire data set with all charts click here
This example is used to illustrate the need for higher
mathematics when one wants more than just a
general idea about what is happening for the function. Concetps
of a limit can be discussed an
estimate of the derivative can be calculated (at least
estimated with this data set) and a derivative at a
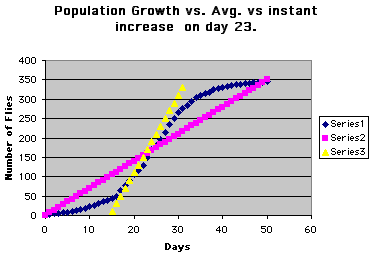
certain point can be compared to the whole. Below we estimated
the instantaneous rate of change
on day 23 (growing about 20 flies per day) and ploted it against
the graph of the entire function
and the average growth rate.
To see the entire data set and charts using the estimated
derivative click here
Question
Is this growth or rate of increase similar to financial
growth or any other type of function ?
* Growth of a fruit fly population in a controlled experiment.
(Source: Elements of Mathematical Biology by A.J. Lotka,
1956, Dover, New York, p.69.
Return