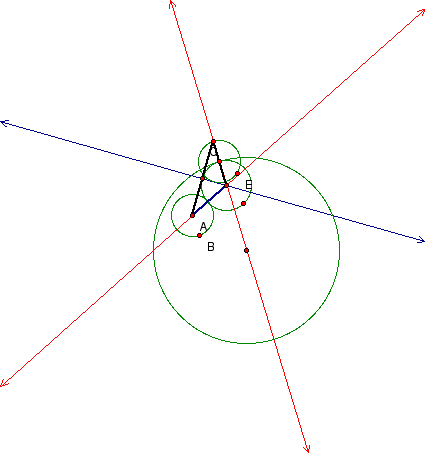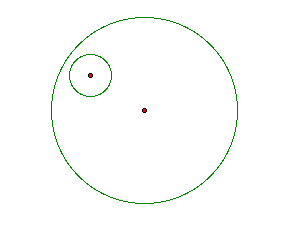
Geometry sketch pad allows many approaches of solving the above problem for a variety level of students.
-Less experienced students may take a hit or miss approach taking advantage of an electronic
drawing program's forgiving features.
-Immediate or advanced students may take a logical or even an analytical approach to produce exact
results.
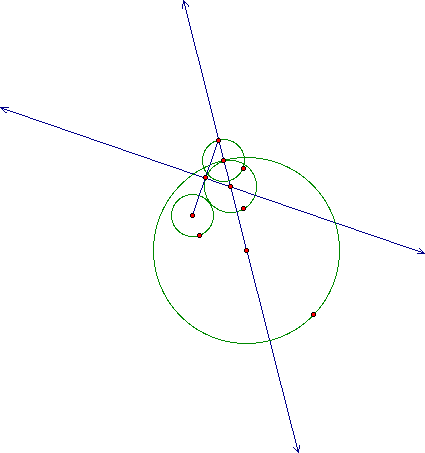
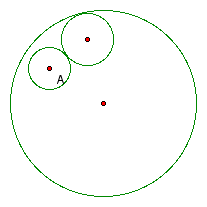
Notice below , the isosceles triangle formed from midpoints and radii of the circles in question. Notice also, that the created tangent circle with point E is divided
into 6 equal pieces by the three intersecting lines. Further finding relationships of this type (triangles, circles, and parallelsim) is a continuing challenging feat.