Consider the acute triangle ABC below along
with it's circumcircle, points of
intersection with altitudes, and orthocenter H.
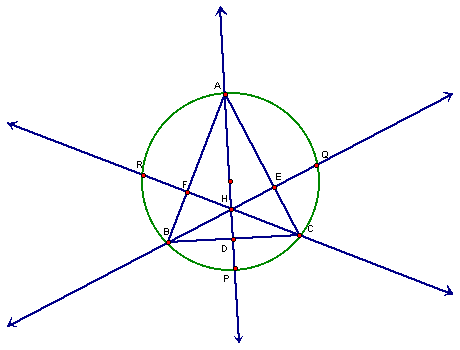
There are numerous relationships to notice. To point
out and persuade about a few
details lets also examine the triangle constructed from where
the extended altitudes
meet the circumcircle and create triangle RQP.
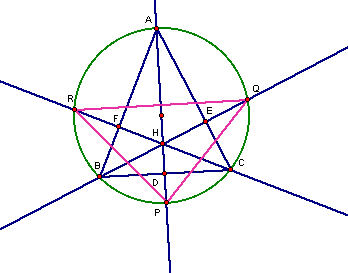
What do we notice about this?
If we construct another triangle with points EFD we
notice that the points are simply
the midpoints of segments of equal length that are intersections
of triangles ABC and
RQP.
This will be the orthic triangle
below
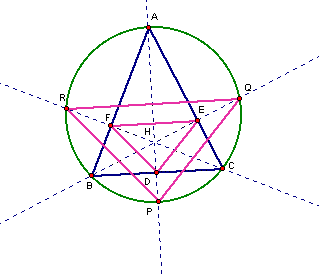
Will this always hold?
Will pointsEFD always be midpoints
of their respective segmenst?
Click here to make some general
observations when working with the obtuse situation.
(Hint: grab any angle and pull it out greater than
90 degrees)
We see that if the triangle is right triangle PQR and
EFD become the degenerate
triangle.
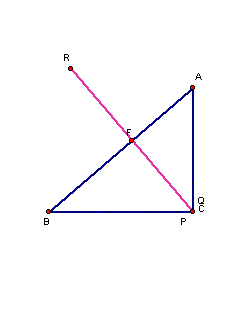and if ABC is obtuse, the relationship of the orthic
triangle and the midpoints of the
intersecting triangle segments fail to exist and we simply
have EDF outside of the
scenario and having different relations altogether.
Return