

We look at the graphs of the following functions...
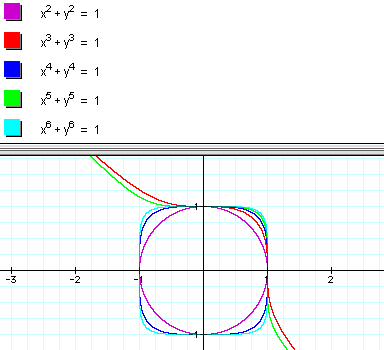
We notice that the even powered functions are "circle like" and as n increases and is even for ,
the graph of the function estimates an almost a perfect square.
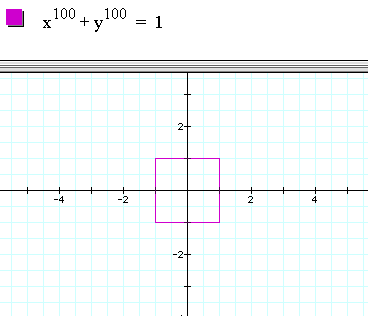
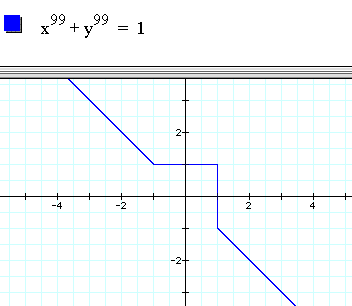
The other case being when the function has odd powers of n and a curve is produced typical to the hyperbolic curves associated with functions of the form
We predict that for very high values of odd n, the curve will begin to resemble a line
that has a component that almost takes on the appearance of a square around (-1,1) through (1,-1).
Graphs for several of the functions in question are graphed all together below.
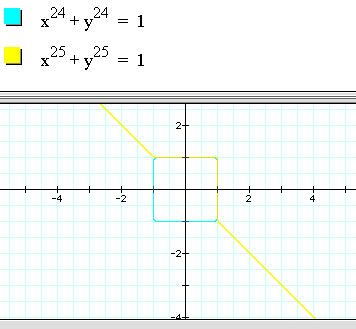
These graphs follow the above predictions for a large odd n and a large even n in the function
Some further explorations would be to evaluate the function as n goes to zero or with n being a rational number, and to calculate the slope of the tangent lines at different points of the function with different n values.
Click here to view movie of the function with changing n values