
We consider a triangle ABC and an arbitrary point P,
inside the triangle.
We draw lines from each vertex of the triangle through
P, and observe as they intersect the
opposite sides of the triangle.
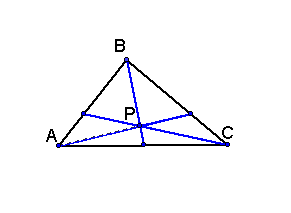
We see 6 to 13 new triangles formed from this new point.
We want to look at some
relationships, so lets consider the sketch as a whole
with the points of intersection of the
sides and lines from each vertex called F, D, E.
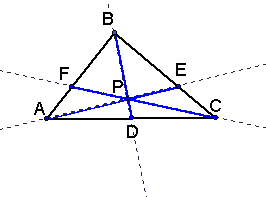
To play with the triangle above and see the measurements
of various segment lengths as the angles change
click here.
We want to pay particular attention to the relationships
of the alternating segments that make up the large triangle ABC.
Specicifically we want to examine
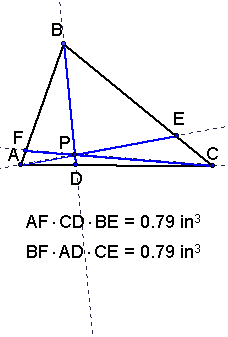
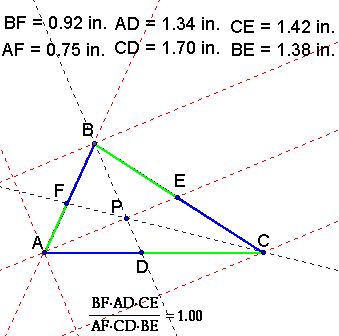
(BF)(AD)(CE) and (FA)(DC)(EB)
to see the values of the products
with different choices of P, click
here
You will find that as long as P, is inside the triangle,
the products are equal. A sample triangle is pictured below.
To further prove this case we first consider that the
ratio of
(BF)(AD)(CE) and (FA)(DC)(EB)
=1
 and
We speculate that shifting P
augments respectivly each alternating segment of the larger triangle,
but why is the product of the
alternating sides always 1?
We try and look for some similar triangles with the
creation of 2 new lines parallel to segment FP and discover the
similar triangles below.
and
We speculate that shifting P
augments respectivly each alternating segment of the larger triangle,
but why is the product of the
alternating sides always 1?
We try and look for some similar triangles with the
creation of 2 new lines parallel to segment FP and discover the
similar triangles below.
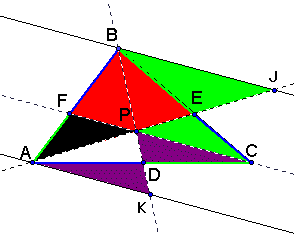 We point out that
We point out that
1. JBE ~ CPE
2.CDP~ ADK
3.AKB~ FPB
4. BJA~ FPA
Click here to explore the similar triangles
From the above ratio (BF)(AD)(CE) /
(FA)(DC)(EB) =1, using a variety
algebraic
steps and set ups we want to show
(BF)(AD)(CE) = (FA)(DC)(EB)
using the following ratios of
similar triangles leads us to many methods to show the desired
outcome.
(AD)=(AK)(CD)/(PC)
(BF)=(FP)(BA)/(AK)
(CE)=(BE)(PC)/(JB)
(CD)=(AD)(PC)/(AK)
(FA)=(FP)(BA)/(BJ)
(BE)=(CE)(JB)/(PC)
One particular dirction leads to
(FP)(BA)(AK)(CD)(BE)(PC)/(AK)(PC)(JB)
=
(AD)(PC)(FP)(BA)(CE)(BJ) /(AK)(BJ)(PC).
After some lengthy work by substitution,and multiplying by inverses
you may arrive at several results which should be equivalent to
the original conjecture.. that
(BF)(AD)(CE) - (FA)(DC)(EB) =0
=>
(BF)(AD)(CE) = (FA)(DC)(EB) and
(BF)(AD)(CE) / (FA)(DC)(EB)
=1.
We want to last construct a new triangle using the
points of intersection FDE that will have an interior point P.
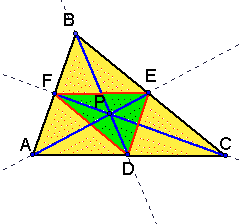
We want to look at the areas
of triangle ABC and FED and compare. For different values of P...
Is there a minimum ratio?
Is there a maximum ration?
Where do these occur?
Click here to manipulate P, and
see the areas of the triangles vary.
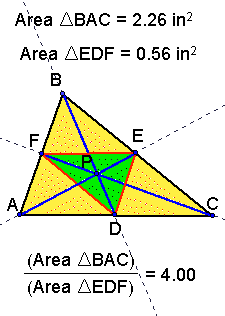
From this exercise we see that the ratio of the two
triangles will always be greater than or equal to 4 when P is
inside the triangle. The minimum ratio of 4 occurs when P is the
orthocenter, and the maximum occurs (when EFD is the smallest
as possible)...
The Minimum ratio (P is the orthocenter)
 Tha Maximum ratio occurs when EDF is the degenerate
triangle, and as the area approaches this limiting value the ratio
approaches infinity.
Tha Maximum ratio occurs when EDF is the degenerate
triangle, and as the area approaches this limiting value the ratio
approaches infinity.
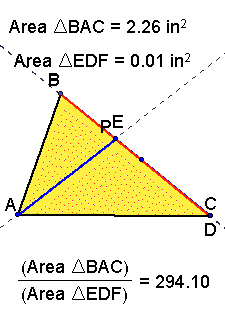
The above cases of area are only generalized for the
case where P is on the triangle or inside the triangle. If P is
outside the conjecture does not hold and the geometry then becomes
more complex and outside the scope of this investigation.
Return










