

Let's graph a few examples of this equation and see if we can find any recurring patterns in the graphs. We'll start with the circle:

Next, we can show the graph when n=3 along with this circle:
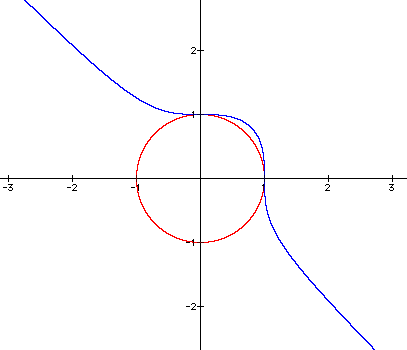
So, when we take the graphs with n=2 and n=3, it looks like we get two points of tangency for the two equations. One point seems to be at x=0 and the other at x=1. It also appears that our equation when n=3 is asymptotic to the line y = -x. Let's check that in a graph.
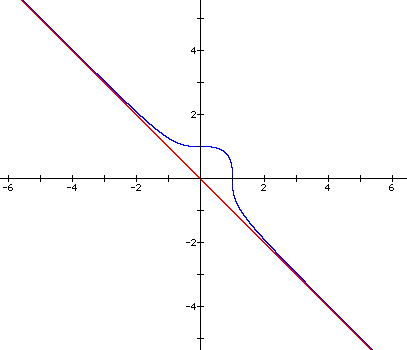
It looks like we do have an asymptote here. To show this, the graph was zoomed out some to show higher values of x and y.
Next, let's see what kind of graph we get when n=4.
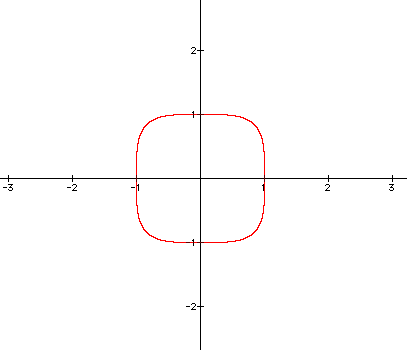
Now, instead of a smooth circle, our equation is leveling out some to look more like a square. Does this graph have any obvious relationships to when n=3?
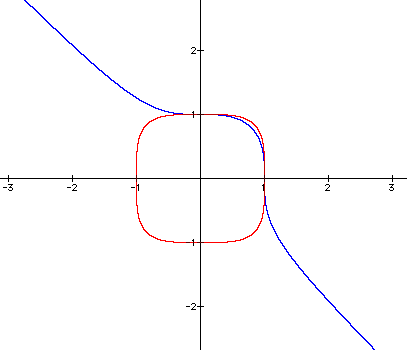
Now, the graph with n=3 may still be tangent to our graph with n=4 and it looks like it is still asymptotic to y = -x. But, the graph when n=3 has moved inside the rounded graph when n=4.
Let's add an equation with n=5 to see what that does.
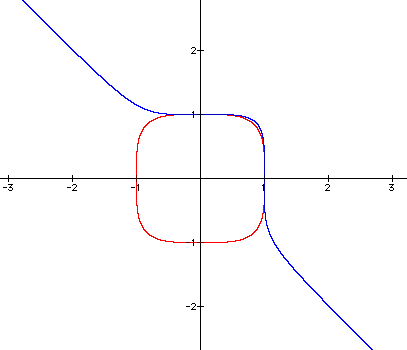
This appears to be a similar case to when we had n=2 and n=3. Again, the graphs look to be tangent at x=0 and x=1, and there seems to an asymptote to y = -x.
What would happen as n continues to increase? What prediction would you make if we took n=24 or n=25? Our guess might be that as we kept getting larger even exponents, the circle we started with would continue to move more and more towards a square. And, as we get the next odd exponent, we would expect that its graph would come closer to outlining our new graph with the even exponent, would be tangent to it at x=0 and x=1, and again be asymptotic to y = -x.
Let's take n=24 and n=25 to see if these assumptions are true.
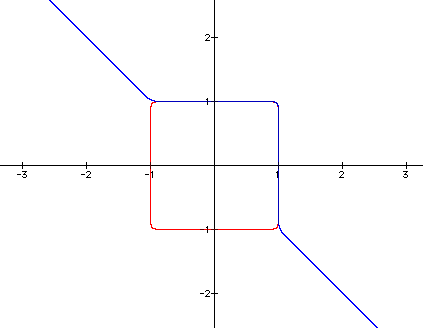
We have taken a few examples of a particular form of equation and been able to make a generalization to know what happens with different values of n.