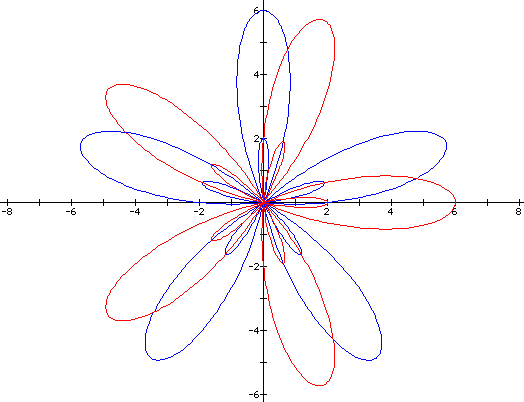
In this assignment, we will look at how changing the variables in polar equations affects the graphs of those equations. We will start with the equation:
This graph will form a number of leaves, which depends on the value of k. If a and b are equal, the graph will have exactly k leaves. For example,
Click here to see this graph in motion as a and b are kept constant while k ranges from 0 to 8. New leaves are formed as k increases.
What happens when a and b are not equal to each other? The values of a and b affect the size of these leaves. Also, these variables determine if there will be an extra set of leaves along with the original k leaves or not. If a is greater than b, we will again have a graph with k leaves. The shape of the leaves and how close their vertices come to the origin depend on how much bigger a is than b.
Click here to see the graph change as b is varied as a lesser value than a.
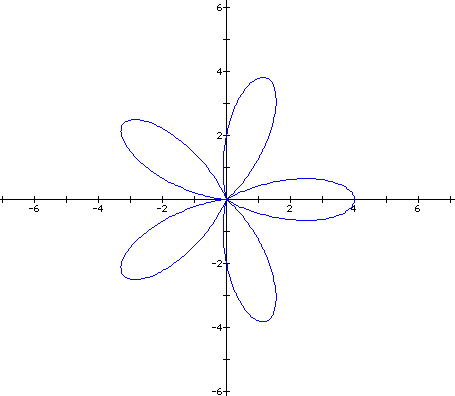
If a is less than b, a second smaller set of k leaves will be formed. When k is an odd integer, this second set of leaves will form inside of the others. For example, if a=3 and b=7 for a graph with 5 leaves (k=5), our graph will look like this
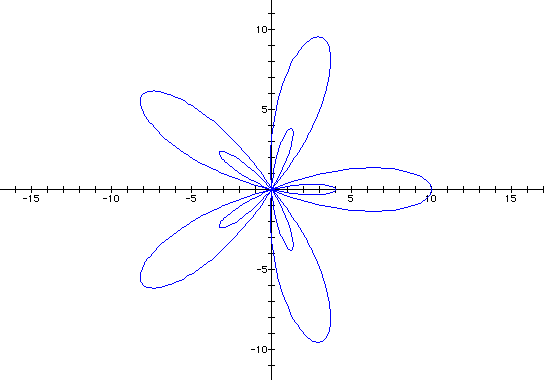
If k is an even integer, the second set of leaves will form between the larger ones. For example,
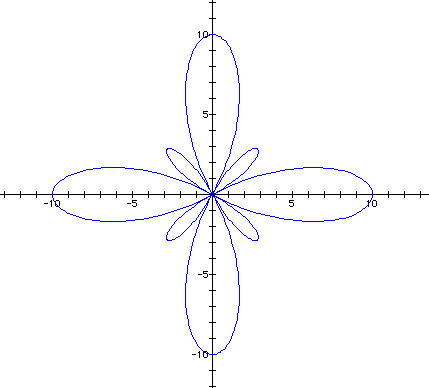
Every equation of this form will produce leaves with that have (a+b) as their maximum distance from the origin. The difference in the values for a and b will determine how much bigger one set of leaves is than the other.
Click here to see the leaves change size as a is varied as a lesser value than b.
This shows a ranging from 0 to the value of b (7 in this example). When a reaches 0, the graph will have 2k leaves which have a maximum distance of b from the origin. When a is equal to b, the graph will expand to be a distance of 2k from the origin with (a+b) leaves.
So, whenever there is an equation of this form in which a=0, its graph will have 2k leaves and have a maximum distance of b from the origin (which is still a+b because a=0 now). These equations will look like:
How would these graphs be different if sine were used instead of cosine? What happens is that the graphs will take on the exact same shape, but they will take on a phase shift where the graph of the equations using sine is a copy of the other just rotated about the origin some. For example,