

To start with this equation, let's fix values for b and c while we vary the value of a. For example, let b = 1 and c = 2.
Here's what a few of these graphs look like for a = -2, -1, 0, 1, 2, respectively.
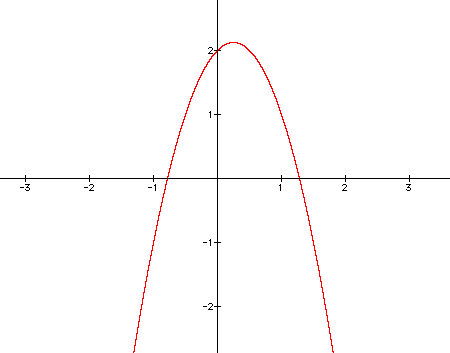
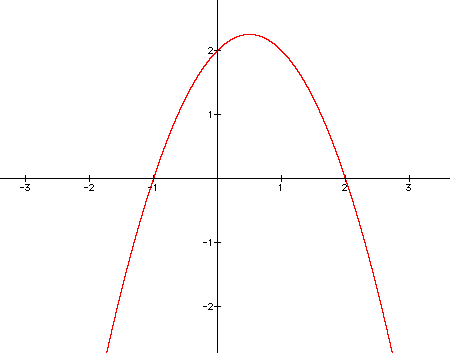
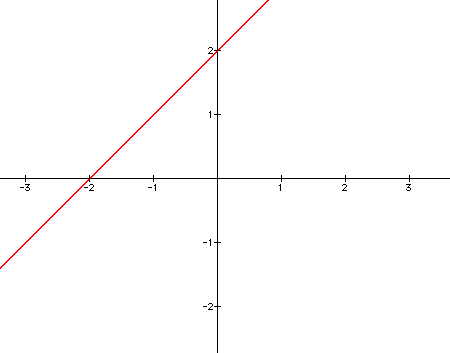
As you can see, when a = 0, our equation is the same as y = x+2, which is a line with a slope of 1 intersecting the y-axis at 2. Let's continue to look at this graph as a becomes positive.
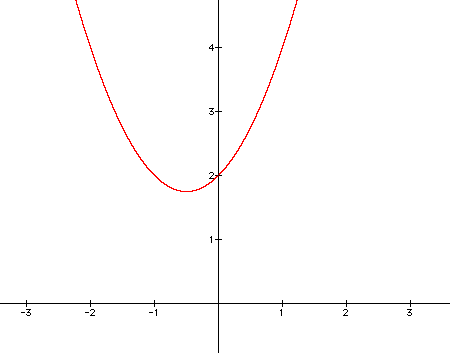
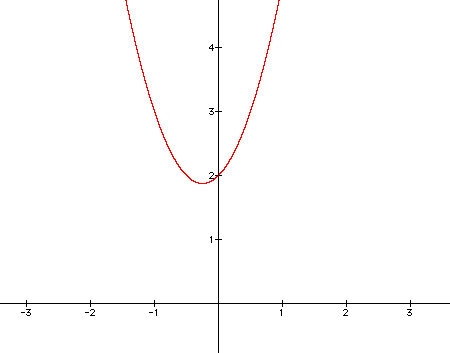
If we look at all of these graphs together, we can really learn about what is happening as a varies. One property that these graphs will all have is that they will all share a point at (0,2). This is true because whenever x = 0, y must equal 2. The value of a does not affect that.
Also, by looking at these graphs in a sequence starting with a being negative and moving into the positives, we see that the graph goes from concave up to concave down. This happens because of the second derivative of the equations. If the second derivative is negative, that implies that the original graph is concave down. When a is negative in our equation, the second derivative will always be negative. Just the opposite is true for a positive second derivative, which will happen when a is positive.
To get a better idea of how this curve moves, we can look at it in motion as the value of a ranges from -2 to 2. This shows how the parabola flips when the value of a crosses from negative to positive or vise versa. As that value gets further away from zero, the parabola becomes narrower. It is also easy to see that (0,2) is a shared point on the curve for every value of a.
Let's now look at what happens when b and c are both negative and a is varied. We'll try
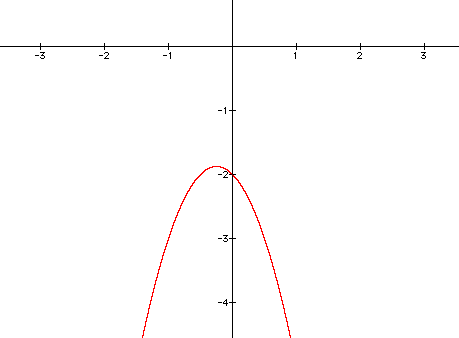
As a becomes more positive, the graph will begin to curve up. When a is at zero, we will get a downward sloping line because our equation will be y = -x - 2. Then, as a becomes positive, the graph will be concave up and will still have a point at (0,-2). That will be the common point for all equations with b = -1 and c = -2.
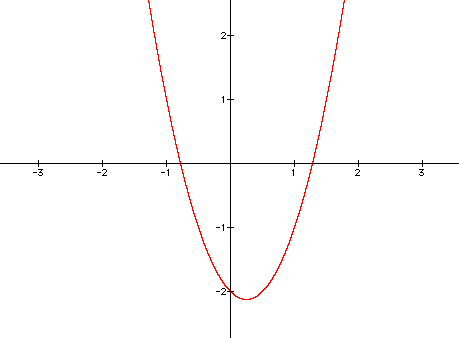
So, this project has shown us that the value of a determines how wide or narrow our parabola will be when we have an equation of the form: