

If we are given two circles, we can pick a random point on either of those circles and create a circle with that point as its center which is tangent to both of our original circles. Here is an example of that:
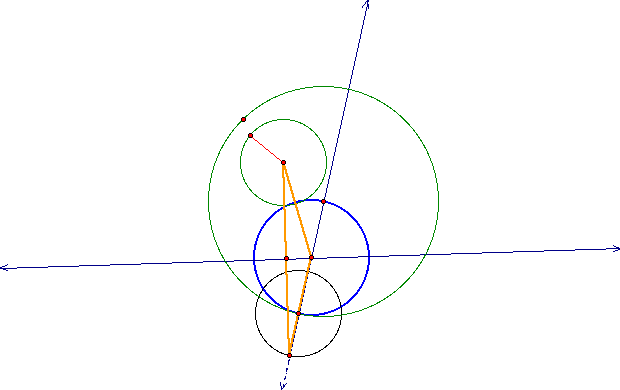
Here, the two green circles are our original circles and the thick blue cirlce is the one that will be tangent to those two. The random point that we picked on one of the green circles was used as the center of the black cirlce to create an isosceles triangle (outlined in orange). Click on the following link to see our point move around the original circle. You will see that the blue circle remains tangent to both of the originals at every point. In this link, you can also use the toolbox to create your own tangent circles. Just select that tool, click and drag your first circle, and then click and drag your second circle.
As the center of the constructed circle is traced, it seems to form an elliptical figure. The segments from the centers of our two original circles to the center of our constructed circle will always be the sum of the radii of the two originals, which makes them the foci of our ellipse.
We can move the smaller circle outside of the larger one and repeat the same trace to see what happens. Tracing the point will produce a hyperbola with foci at the centers of the two original cirlces. That hyperbola is in red in this picture. Again, the green circles are the originals and the blue circle is the one which is tangent to those two.
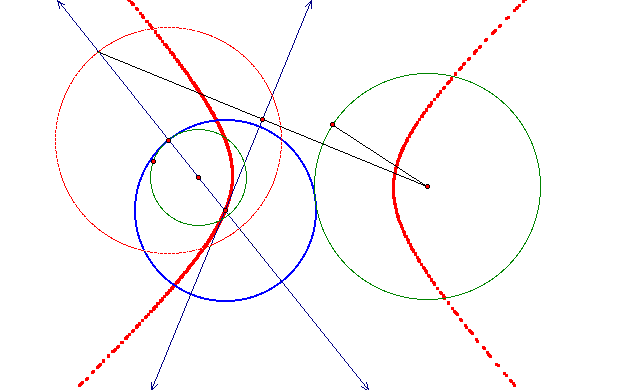
Creating a hyperbola by circles exterior to each other
Let's now trace the line which is perpendicular to the base of the orange isoscles triangle to see how it outlines this ellipse.
Let's now look at the case when we choose our random point on the smaller of the two circles. Again, our original circles are green and the constructed circle will be blue. As the center of the blue circle is traces, another ellipse will be formed. The ellipse is in red from tracing the center of our constructed circle.
Tangent circle (point on smaller circle)
We can also move the smaller circle outside of the larger and see what happens. As the center of the constructed circle is traced this time, it will form a hyperbola with foci at the centers of the two original circles.
Tangent circle (point on smaller circle, which is external to the larger one)
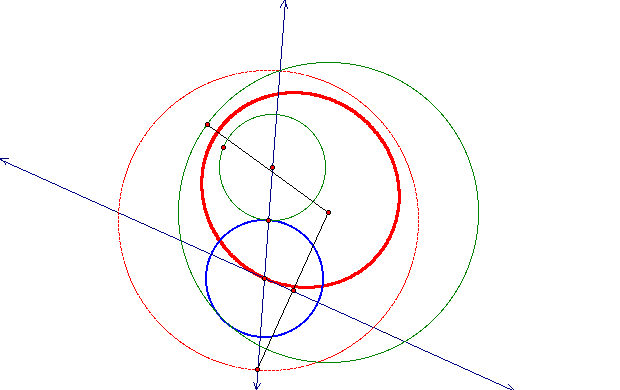
One other case we can examine is when the two original circles intersect. First, let's place our random point on the bigger circle. This, too, will form an ellipse with the centers of the two original circles as foci, but the ellipse will be more stretched out than we have seen with the other cases. The ellipse is in red again. Also, the isosceles triangle is outlined in orange, which is kept in tact as the point moves around the circle.
Creating an ellipse with intersecting circles
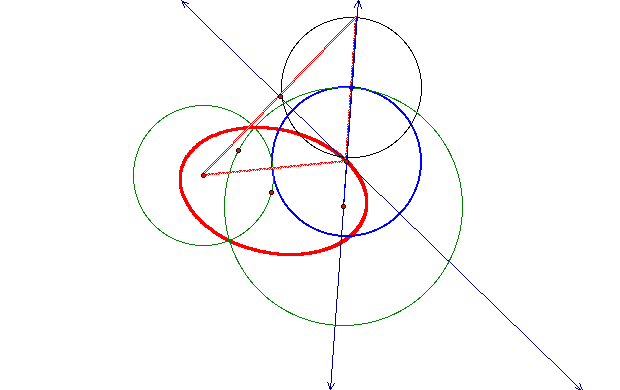
Now, if the point is on the smaller of the circles, our trace will result in a hyperbola, which is in red below.
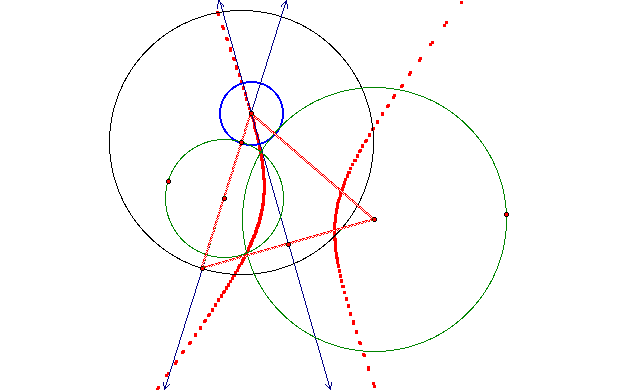
Creating a hyperbola from intersecting circles