Let's take a triangle ABC and construct its orthocenter, H. Next, let's find the orthocenter for the triangles HAB, HAC, and HBC. For example, the orthocenter of triangle HAB is C of the original triangle ABC. This happens because H is on the altitude dropped from A to BC and when a perpendicular is dropped from H to AB, C must be on it because H is on the altitude from C to AB. Since C is on the two of the altitudes of traingle HAB, it is the orthocenter of that triangle (which implies that C is also on the third altitude). Similarly, B is the orthocenter of HAC, and A is the orthocenter of HBC.
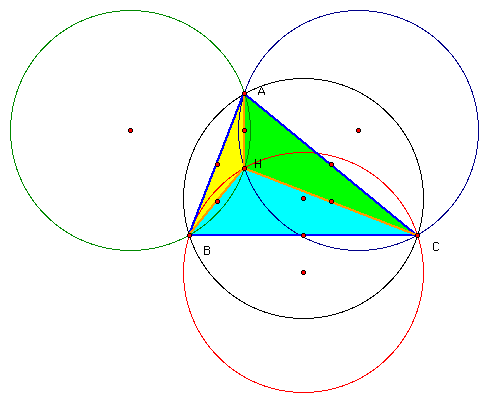
This picture shows us another interesting thing. The circumcircles of all the triangles with the exception of triangle ABC pass through H because it is a vertex, and by definition, circumcircles pass through all the vertices of that triangle.
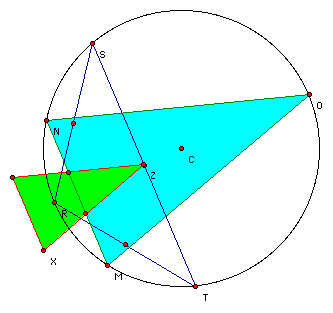
Now, we'll compare the orthic triangle of RST to the triangle which is formed by extending the altitudes of RST to its circumcircle. In the picture C is the circumcenter, XYZ is the orthic trianlge, and MNO is the triangle created by the extended altitudes.
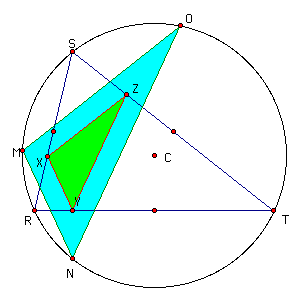
This picture shows that the sides of triangle MNO are parallel to the sides of triangle XYZ. We know that M and X are collinear since they are both on the altitude dropped from T to RS. Similarly, N and Y are collinear and O and Z as well. The lines can be proven to be parallel by using the alternate interior angle theorem. For example, the line RO would be the transversal crossing XZ and MO, which would create congruent alternate interior angles. Also, the area of the orthic triangle (XYZ) is one-fourth the area of triangle MNO. These conditions will hold at all times. Let's look at what happens when trianlge RST becomes obtuse. This makes the orthic triangle move outside of RST because the altitudes do not intersect on the segments. Here is a picure when triangle RST is obtuse.
Click here to open a GSP sketch that you can play with.