

If we have any triangle ABC, we can construct a pedal triangle with any point, P in that plane. Just place a point P and draw perpendicular lines to the sides of ABC (the sides may need to be extended to lines to find intersection points). These three points of intersection will form what is called the pedal triangle.
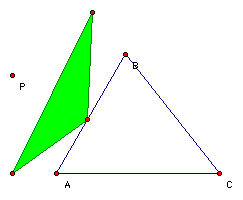
Click here to open a GSP file and experiment with the pedal point.
Next, let's construct a circle around triangle ABC which has its center at the circumcenter but has a radius larger than the circumcircle. We can locate the midpoints of the pedal triangle and trace them as P is moved around the constructed circle. As P is moved around the circle, the trace of the midpoints will form three ellipses.
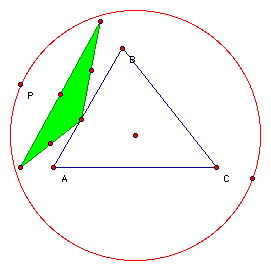
Click here to go to this file and move P around the cirlce.
Now, let's examine what happens when triangle ABC is right or obtuse. When it is right, the midpoints will form two ellipses and the other trace will make a circle. When it is obtuse, we go back to having three ellipses.
Click here to see the trace when ABC is right.
Click here to see the trace when ABC is obtuse.
What would happen if we made P move around the circumcircle and not the circle we constructed? The pedal triangle will become a line instead of a triangle now, but we can still trace the midpoints. The results for the different triangles will be the same as above except that the ellipses or circles formed will all pass through one vertex of triangle ABC in every case.
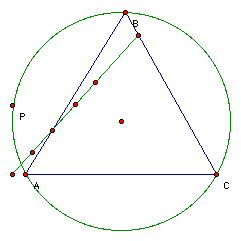
Click here to open a file and experiment with the case when we are using the circumcircle.