

In this assignment, we will investigate more properties of triangles. For example, if given any triangle ABC and a point P inside of that, we can create lines from the three vertices through P. Then, we can create points D, E, and F as the intersections of those lines with with the sides of the triangle where they are on the sides opposite the vertices A, B, and C, respectively. There is an interesting property with this situation. It turns out that (AF)(BD)(CE) = (BF)(CD)(AE).
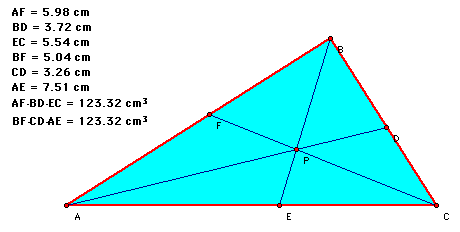
Click here for the proof that (AF)(BD)(CE) = (BF)(CD)(AE).
Click here to experiment with a GSP sketch involving this proof.
Now, we need to check to see what happens when P is outside of the triangle ABC. Interestingly, the same condition holds.
Click here to open a GSP sketch and move P in and out of the triangle and see that the equality holds.
When P is inside triangle ABC, we can create triangle DEF as well. The ratio of the areas of these two triangles will always be greater than or equal to 4. If we make D, E, and F the midpoints of sides BC, AC, and AB, respectively, the ratio of these areas will be equal to 4. This means that P will be the centroid of triangle ABC.
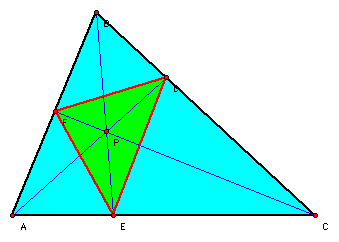
Click here to explore with this sketch.
Click here to see the sketch when P is the centroid.