Polar Equations

By Donna Greenwood

In this assignment, I use Graphing Calculator 3.1 and GSP 4.0 to look at variations of the polar equations r = a + b cos (kq) (the purple graph in these illustrations), r = a + b sin (kq) (the aqua graph) and r = b cos (kq) (the blue graph) for varying a, b and k. The graphs vary in appearance when a < b, a = b and a > b, so we'll look at those three cases. GSP can also be used to graph polar equations, so I’ll compare the two software tools.

In this graph, a = 1, b = 3 and k = 1. The aqua and purple graphs have a loop within a loop while the blue does not.

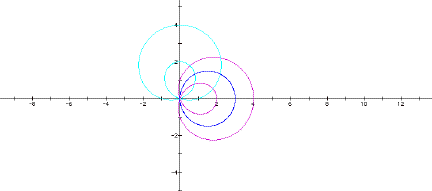
Just to compare the appearance of the graphs, I also graphed these 3 equations in GSP.  Click here for that graph.
 
 

 

The graphs themselves don’t differ too much in appearance, and it’s nice to be able to use GSP for this exploration. GSP is a bit “clunkier” to use when graphing multiple equations on a single graph, because the colors of the graphs all remain constant until changed by the user, unlike Graphing Calculator. However, I like the animation features better in GSP. Click here for a GSP sketch that has the b value replaced by parameters which can be independently animated. 

What happens in this graph if k is not an integer? Here k = 1.5:

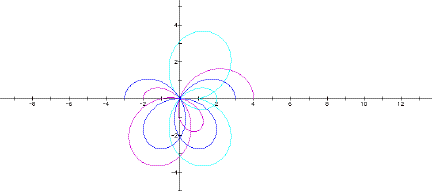
In GSP I used parameters as the k values, and set up separate animation buttons for each graph. The k values vary between -10 and 10. Click here  to watch the graphs “draw and undraw” themselves. If you play with this graph, hide two of the graphs (click on the graph and select “hide function plot” under the Display menu; select “show all hidden” when you’re done) and watch the third. Hide and unhide your way through all three graphs to see the differences. I don’t know if Graphing Calculator has a feature like this, but I had fun watching how the graphs changed as the k values varied. I could also watch for interesting points, like k = 0, and what happens as k approaches 0 from the positive and negative directions.

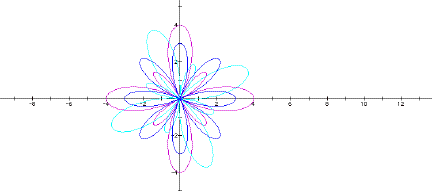
Now look at graphs with a = b. In the first, let a and b be 2, with k = 1.

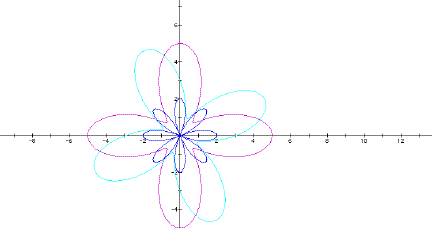
Now increase k to 4.

When k is not an integer, the same sort of thing happens as did when a < b.

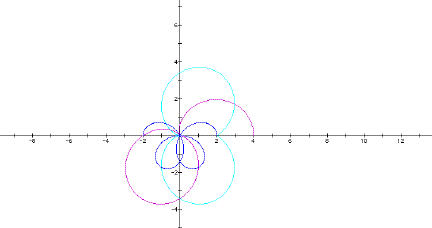
Here’s a GSP sketch  for this graph. In this one, I used parameters for k as in the previous sketch, but I varied the parameters discretely rather than continuously. That makes it clear that k governs the number of petals in the purple and aqua graphs. However, in the blue graph, when k is odd, the blue graph has k petals; when k is even, the blue graph has 2k petals. 

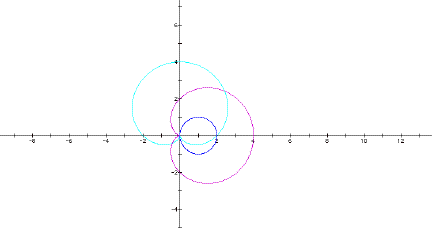
Finally, let a > b. When k = 1, a = 3, b = 2

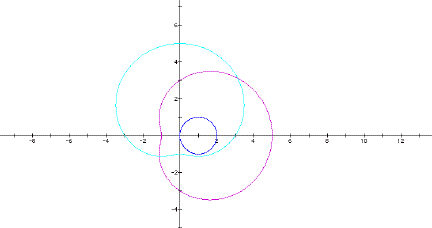
When k = 4

What if k is not an integer? Here k = 1.5:

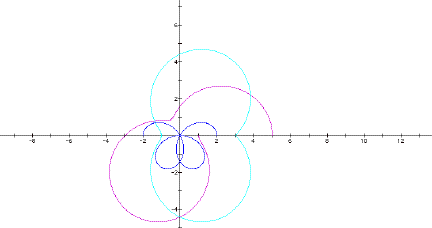
In the cosine graphs (blue and purple), the sign of k makes no difference. But in the sine (aqua) graph, it should. Does it? Click here  for the GSP sketch to explore.  Look at the aqua graph for values of -2 and 2 to validate your theory. It's easy to see because the values of k iterate discretely.

That’s it! I didn’t intend it, but this exploration turned out to be more of a GSP vs. Graphing Calculator comparison than I intended. One of my favorite features of Graphing Calculator is that it automatically generates each new graph in a different color. It’s not shown in this write-up, but Graphing Calculator also does a wonderful job of 3D graphs. GSP is very widely available, and has lots of animation capabilities. In the end, it’s nice to know that’s there is more than one way to explore and present polar equations!