
Explorations
With Parabolas
By Donna Greenwood
A
parabola is graphed in the xy plane as the equation y = ax2
+ bx + c, for any rational numbers a, b and c. Looking at how the graphs
change as two of the values are held constant while the third varies provides
interesting insights.
The
first set of graphs hold b (=1) and c (=1) constant as a is varied.
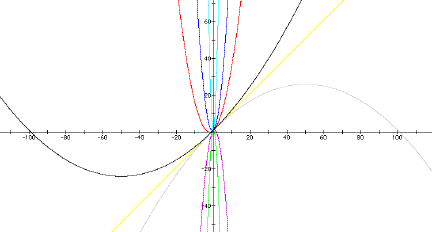
The
yellow line is of a=0. The parabola degenerates into a line, as we would
expect. The gray and black graphs are of a = -.01 and .01 respectively.
The red, blue and aqua graphs are of a = .5, 1 and 10 respectively. The
magenta and green graphs are of a = -1 and -5. The sign of the x2
term determines whether the resulting parabola is a “positive parabola”
or a “negative parabola,” that is, whether the parabola opens up or down.
The coefficient of the x2 term determines how “wide” the parabola
is. Smaller coefficients yield more open, gently sloping parabolas, while
larger values create narrow, sharply steep curves.
These
graphs all intersect at (0, 1), the y-intercept of the graphs. If c were
equal to 0 for all these equations, the intersection point would be the
origin.
The
second set of graphs hold a and c constant at 1 as b is varied.
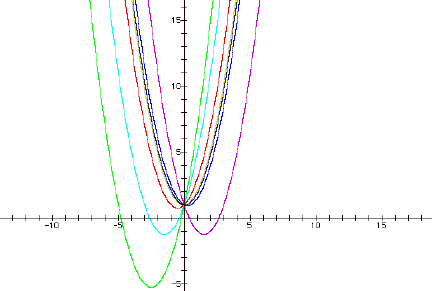
The
magenta graph is b = -3; the red is b = 1, the blue is b = -.5, the green
is b = 5; the aqua is b = 3, the yellow is b = 0; the gray is b = .1 and
the black is b = -.1. From this we can see that negative b terms (magenta,
blue and black) have their vertices in positive x quadrants ? I and IV,
while equations with positive b terms have vertices in negative x quadrants
? II and III. This makes sense when you remember that the x-coordinate
of the vertex is given by the equation ?b/2a. The y-coordinate of the vertex
is found by replacing x in the original equation and solving for y. So,
in large part, b determines where the vertex of the graph lies.
As
with the first set of graphs, these graphs all intersect at (0, 1) which
leads to the conjecture that the c term determines where the graphs intersect.
Finally,
looking at the special case where b = 0 (the yellow graph, which is in-between
the gray and black graphs) doesn’t really show anything new. The equation
of the graph is y = x2 + 1, with the vertex at (0, 1).
The
third set of graphs hold a and b constant as c is varied.
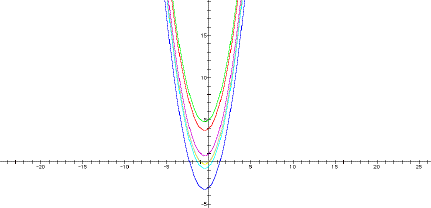
These
graphs don’t intersect as the other sets of equations did. This is because
the c term governs the y-intercept, and that term varies in this set of
graphs. The variation in the c term moves the parabolas up or down the
y-axis. The y-intercept for a quadratic in the form y = ax2
+ bx + c has its y-intercept at (0, c).
These
parabolas all have the same shape and orientation, due to the constant
a and b terms.



