Altitudes and Orthocenters

By Donna Greenwood

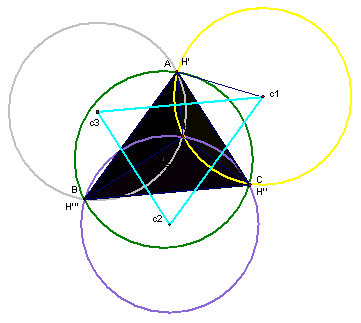
Given a triangle ABC, construct its orthocenter (call it H), then construct the orthocenters of all the 'subtriangles' formed by the orthocenter and two of the vertices of the triangle - HAB, HAC and HBC to be precise. Notice that the orthocenter of the subtriangle is the missing vertex. For triangle HBC, the orthocenter is point A (also labeled H'). For HAB, the orthocenter is point C (also labeled H''). For triangle HAC, the orthocenter is point B (also H'''). Next, construct the circumcircles of each of the four triangles. If you connect the centers of the circumcircles of the subtriangles and construct the orthocenter of that triangle, the orthocenter is the circumcenter of triangle ABC. Click here for the sketch.

Can we prove any of this? It looks like there are two conjectures to prove. First of all, are the orthocenters of the subtriangles really the missing points, or is this a cruel joke that GSP is playing on me?

Here's a simplified picture to help with the proof. Show that DHBC's orthocenter is a vertex A, then extend that to the other subtriangles. Take as given triangle ABC and point H as the orthocenter of triangle ABC. The altitudes from C to side AB, B to side A and A to side BC are shown as well.

By definition, the orthocenter of a triangle is the intersection of the lines containing the altitudes of the triangle.  An altitude is a perpendicular segment from a vertex to the line defined by the opposite side.

To show that the orthocenter of triangle HBC is vertex A, consider the following. Triangles ABC and HBC share side BC, and H falls on the altitude from A to BC by definition. Therefore, the altitude from H to BC is the same line defined by A to BC. Next, again by definition, the altitude defined by CH is perpendicular to side AB of triangle ABC. The altitude from B to side CH of triangle HBC is then side AB, by definition of altitude, and because there cannot be two lines perpendicular to a line through a single point. Likewise, the altitude from C to side BH is side AC. It follows that lines defined by AB, AC and AH intersect at A, making A the orthocenter of triangle HBC.

Repeating the proof for triangle HAC proves that the orthocenter is B, and C for triangle BAH.

The second conjecture that's been made is that the triangle with vertices at the circumcenters of the subtriangles (call it DDEF) has the circumcenter of triangle ABC as its orthocenter. Here's a picture with the circumcircles hidden and some construction lines added. The circumcenter of the black triangle (DABC) and the orthocenter of DDEF is labeled G. Take as given that G is the circumcenter of DABC and prove that G is also the orthocenter of DDEF. To prove this conjecture, show that G is on the altitudes of DDEF. It will be most helpful to show that DDEF is congruent to DABC and that corresponding sides of these triangles are parallel (for example, show DE || to BC).

First, here are some general observations.

1. AD = BD as radii of the circumcircle of DHAB. Likewise, AE = EC and CF = CB as radii of the circumcircles of triangles HAC and HBC. Finally, GA = GB = GC as radii of the circumcircle of DABC. This gives lots of isosceles triangles.

2. Look at quadrilateral ADBG. Its diagonals are AB and DG. Those diagonals intersect in a right angle, since G and D fall on the perpendicular bisector of AB by definition of the circumcenter. Diagonals that intersect at right angles determine a rhombus, so ADBG is a rhombus:  a figure with four congruent sides whose opposite sides are parallel. This same reasoning can be applied to give rhombi AGCE and GCFB.

3. By definition of a rhombus, AD = BD = GA = GB and AD || BG and BD || GA for rhombus ADBG. Similarly, GA = GC = AE = EC and GA || EC and AE || GC for rhombus AGCE. For rhombus GCFB, GB = BF = FC = GC and GB || FC and BF || GC.

4. Finally, since each pair of rhombi share one side, all the sides listed above are congruent. In addition, AD || EC since both are parallel to GA.

To begin, prove that DE || BC. Here is the same diagram with more lines hidden and some angles labeled.  For clarity, let a represent angle BEC; b represent angle EDB; c represent angle BCE; d represent angle DBE; e represent angle BED; and f represent angle EBC.

Quadrilateral BDEC has one pair of parallel, congruent sides, EC and BD. Then the measure of angle b + the measure of angle e + the measure of angle a = 180 degrees using DE as a transversal, as same side interior angles of EC and BD.Likewise, the measure of angle c + the measure of angle d + the measure of angle f = 180 degrees using BC as a transversal. 

Draw in diagonal EB. EB is also a transversal of parallel sides EC and BD. As alternate interior angles, angle a @ angle d. That gives DDEB @DCBE by SAS (shared side BE; measure of angle a = measure of angle  d and BD = EC). Therefore, ED @ BC, angle b @ anglec and angle e@ angle f as corresponding parts of congruent triangles. That gives the measure of angle b + the measure of angle d + the measure of angle f = 180 degrees after substitution.  This gives same side interior angles for parallel lines DE and BC with BD as a transversal. Therefore, DE || BC.

The same logic can be applied to quadrilateral DACF to give AC congruent and parallel to DF; and to quadrilateral AEFB to give AB congruent and parallel to EF.So DDEF is congruent to DABC and pairs of sides of the triangles are parallel.

G is the circumcenter of DABC. As such, it lies at the intersection of the perpendicular bisectors of sides AB, BC and AC, and is equidistant from vertices A, B and C. Vertices D, F and E also lie on the perpendicular bisectors of AB, BC and AC, as the circumcenters of DAHB, DBHC and DAHC respectively.

It follows that DG^ AB. Since AB || EF, DG ^ EF. Therefore, G lies on the altitude from vertex D to side EF. Similarly, EG ^ AC and EG ^ DF, so G lies on the altitude from vertex E to side EF. Finally, FG^BC and FG^DE, so G lies on the altitude from vertex F to side DE. Therefore, G is the orthocenter of DDEF by definition.

 

Final Notes (alternately titled 'Things I Noticed, But Have No Intention of Proving')

1. DDEF is not only congruent to DABC, it is a half turn rotation (180 degrees) from DABC. The center of the rotation is at the midpoint of the segment from the orthocenter of DABC to its circumcenter (midpoint of HG in the sketch above).

2. The areas of all the circumcircles are the same. This falls out pretty easily when you show that the radii are all the same.