Pedal Triangles

By Donna Greenwood

LetDABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing the perpendiculars to the sides of ABC (extended if necessary) locate three points R, S and T that are the intersections. DRST is the Pedal Triangle for Pedal Point P. Here’s a picture:

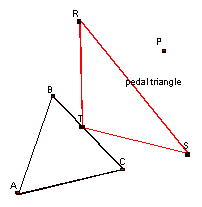
In this exploration, I used several tools from my GSP 4.0 library to explore some special cases of pedal point locations and the resulting pedal triangles. Those tools are replicated in the sketches referenced below if you’d like to validate or explore these conjectures further. To go directly to a case you’re interested in, click one of the links below:

Case I: Pedal Point at Orthocenter

Case II: Pedal Point at Incenter

Case III: Pedal Point at Circumcenter

Case IV: Pedal Point on Circumcircle

Case I: Orthocenter

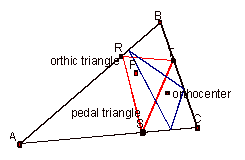
When the pedal point is located at the orthocenter of DABC, the resulting pedal triangle is the orthic triangle. Here are some sketches, but it’s much easier to see for yourself on the GSP sketch:

This sketch shows separate orthic and pedal triangles when the pedal point is not concurrent with the orthocenter. When the pedal point is moved over the orthocenter, the two triangles coincide:

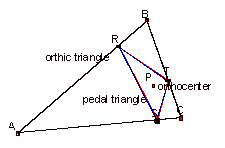
This finding is not very surprising, given the definitions of the orthocenter, orthic triangle and pedal triangle. The pedal triangle is formed by connecting the feet of the altitudes from an arbitrary pedal point P to the (extended) sides of a triangle (ABC). The orthocenter is the intersection of the altitudes from any vertex to the opposite side of the triangle. The orthic triangle is formed by connecting the “feet” of those altitudes. By moving P to the orthocenter’s “spot”, we’ve merely moved the “arbitrary” pedal point to a location where the perpendiculars have meaning ? as the altitudes of DABC.

Case II: Incenter

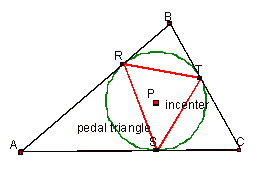
When the pedal point is at the incenter, the pedal triangle is inside DABC, with vertices R, S and T at the points of tangency of the incircle with DABC. Click here for the sketch.

This finding is a little more surprising, but looking at the definitions of incenter, incircle and pedal triangle makes it obvious. The incenter is the intersection of the angle bisectors of DABC and is the center of the incircle, the inscribed circle. As such, the incenter is equidistant from each of the three sides of DABC. The perpendiculars from the incenter to the sides of DABC form intersections with the sides of DABC that are the points of tangency. By moving the pedal point P to the incenter’s location, we have once again, removed the “arbitrariness” of P and placed it in a location where the altitudes have meaning as the radii of the incircle.

Case III: Circumcenter

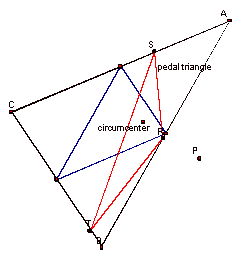
When the pedal point is at the circumcenter, the pedal triangle is the medial triangle. This is true regardless of the location of the circumcenter. Click for a sketch to modify. Here is the sketch with P not equal to the circumcenter:

You can see separate pedal and medial triangles. When P is moved to the circumcenter, the triangles overlay one another as seen here:

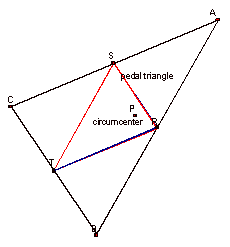
Here is a picture when the circumcenter is outside the triangle:

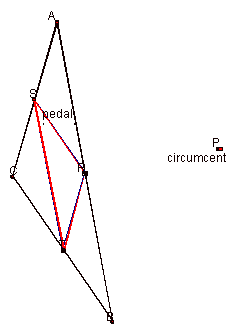
Does this finding fall out as easily from the definitions as the others did? The circumcenter is the intersection of the perpendicular bisectors of the sides of the triangle. It’s also the center of the circumcircle. The medial triangle is the triangle formed by connecting the midpoints of the sides of the triangle. When the pedal point is moved to the circumcenter’s location, the perpendiculars from P to the sides of the triangles are the perpendicular bisectors of the sides, which by definition pass through the midpoints of the sides. It follows that when P is the circumcenter, the pedal triangle is the medial triangle.

Case IV: Circumcircle

When P is on the circumcircle of DABC, the pedal triangle degenerates into the Simson Line. Click here for a sketch you can manually manipulate. Click here for an animated sketch. In this one, the envelope of lines is traced.

Finally, just for fun, here are some animated sketches that trace the midpoints of the sides of the pedal triangle as the pedal point moves about circles that are centered at the circumcenter. The first is a circle smaller than the circumcircle. The second is on the circumcircle and the third is larger than the circumcircle. What shapes are traced out? What differences are there among the traces?