---

Explorations with Ceva’s Theorem and Triangle Areas

By Donna Greenwood

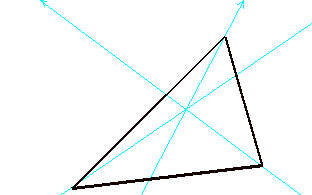
Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP and CP extended to their intersections with the opposite sides in points D, E and F respectively. (1) Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P; (2) Show that when P is inside DABC, the ratio of the areas of DABC and DDEF is always greater than or equal to 4..

Ceva’s Theorem/Ratio Exploration

Here’s a sketch:

Click here for a sketch to experiment with. You’ll see that the ratio of the segments is always 1 when P is inside or outside the triangle. When P is actually on one of the segments of the triangle, the ratio is either zero or undefined. The only way I could see that precisely with GSP was to merge P with one of the segments of the triangle (under the Edit menu, if you’re interested.) Another interesting case is when the triangle is degenerate, that is the three vertices are collinear. Then …

This phenomenon is known as Ceva’s theorem, which states that three lines AD, BE and CF intersect in a single point if and only if (AF/FB)*(BD/DC)*(CD/EA) = 1. The lines AD, CF and BE are known as Cevians, lines in a triangle from a vertex to the opposite side.

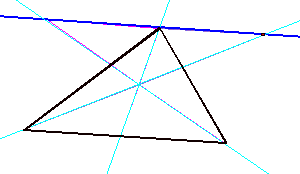
Why does it work? To prove, add a construction line to form similar triangles. Creating a line parallel to BC through A will do it. Let the intersection of the line with extended CF be Q, and the intersection of the line with extended BE be R. This creates lots of “sets” of similar triangles. Here’s a sketch of the first:

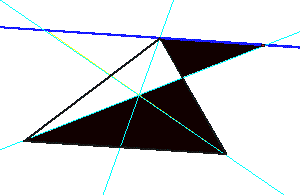
The yellow triangles, DAQF and DBFC are similar (use QC and AB as transversals of parallel lines QR and BC to see this.) Likewise, the gray triangles, DAER and DCEB are similar.

Notice that DAPQ is similar to DDPC (the pink triangles) and that the purple triangles, DAPR and DDPB are similar.

· From the yellow triangles: (AF/FB) = (FQ/FC) = (AQ/BC).

· From the gray triangles: (EC/AE) = (BE/RE) = (BC/AR).

· From the pink triangles: (AP/PD) = (QP/PC) = (AQ/DC), and

· From the purple triangles: (AP/PD) = (RP/PB) = (AR/BD).

The ratios in the pink and purple triangles are all equal, since they have (AP/PD) in common, so we can set (AQ/DC) = (AR/BD). A little algebra gives (BD/DC) = (AR/AQ).

Next, multiply together the bolded terms to get:

(AF/FB) (EC/AE) (BD/DC) = (AQ/BC) (BC/AR) (AR/AQ)

The terms on the right side all cancel out, giving us

(AF/FB) (EC/AE) (BD/DC) = 1!

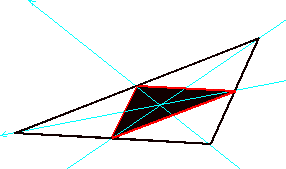
Area Comparison

Here’s a sketch with the area ratio:

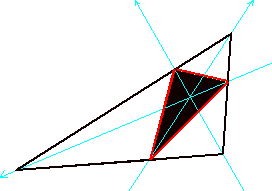
This sketch has the common triangle centers added as well. If you move P over the centroid, the area ratio is always 4. If P is anywhere else within the triangle, the ratio is greater than 4. On this sketch, you can also move P outside the triangle.

So we ask the usual question: why does this work? When P is the centroid, the Cevians are the medians, and D, E and F are the midpoints of the sides of DABC, and the triangle mid-segment theorem comes to the rescue. By that theorem, each of the white triangles (DBDF, DAFE, and DDEC) have a base that is 1/2 the base of DABC and a height that is 1/2 the height of DABC. That gives each of the white triangles an area that is 1/4 the area of DABC, leaving 1/4 of the area in DDEF.

Final Notes

Some interesting extensions of this exploration would be to use Ceva’s theorem to prove that the lines that create the common triangle centers (orthocenter, incenter, circumcenter and centroid) are concurrent. I think this is a great exploration for kids, because Ceva’s theorem is pretty obvious using the measurements on GSP. It’s also an easy proof, once you draw in the right construction line. Have fun with it!