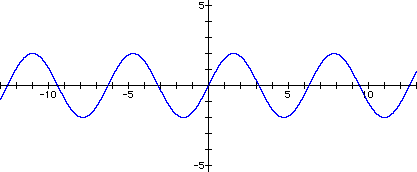
I set b=1 and c=0, which gave the equation y = a sin x. I then tried different values for a and graphed the results. Some examples follow.

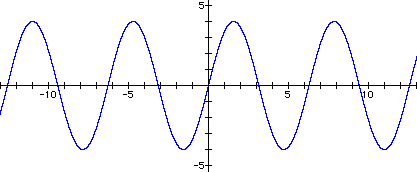
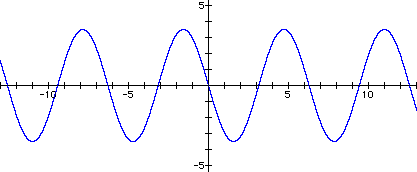
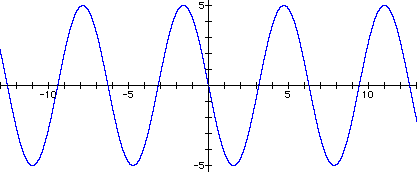
It became clear that changing a caused changes in the amplitude of the equation. In fact, the amplitude of the equation is the absolute value of a. For positive values of a, the graph simply stretched or shrank vertically. For negative values of a, the graph was reflected about the x-axis and also stretched or shrank vertically.
It is also important to note that changing a did not affect the x-intercepts. The x-intercepts are the values of x that will make y = 0. So for y = a sin x we have the following:
If a = 0, then the amplitude of the equation is 0 and we get the line y = 0.
If sin x = 0, then y = 0 regardless of the value of a.
The x-intercepts remain the same for all values of a except 0.
Click here to see an animated graph of this equation.