

Graph several sets of curves for
for selected values of a, b, and k in an appropriate range for t.
We can start by setting the values of a and b and varying the value of k.
If we let a = 1 and b = 1, we get the equations
When t = 0, we get the equations
which define the point (1,1). We can see that for any value of k, the graph will pass through the point (1,1) when t = 0. Since t = 0 will be a common point for all values of k, we will set the range for t so that 0 falls somewhere in the middle. We will try values between -1 and 1.
If we let k = 1, we get the following equations and graph:
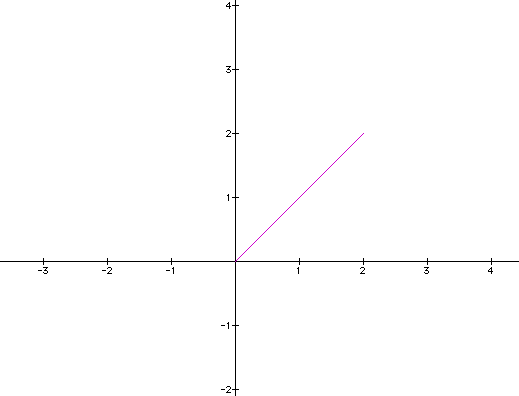
It appears to be a line with a slope of 1.
If we let k = 2 and graph the equation over the first one, we get the following equations and graph:
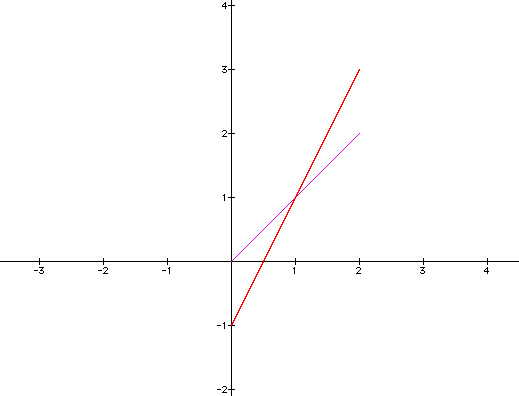
The new graph appears to be a line with a slope of 2.
We see that the two graphs share the point (1,1) as expected.
If we let k = 3 and graph the equation over the first two, we get the following equations and graph:
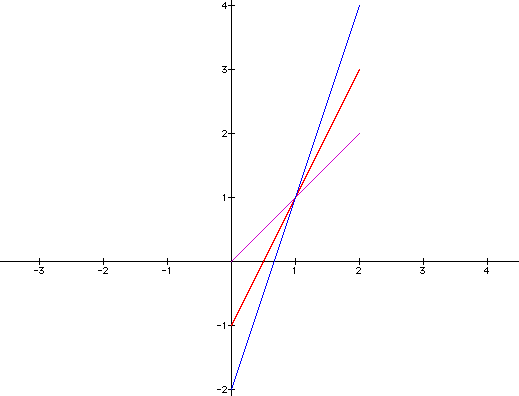
The new graph appears to be a line with a slope of 3.
We see, again, that the graph passes through the point (1,1) as expected.
Looking at our original equations
it seems that they represent a line with a slope of k that passes through the point (a,b).
We will now try different values for a, b, and k to see if this holds true.
If we let a = -2, b = 1, and k = -1, we get the following equations and graph
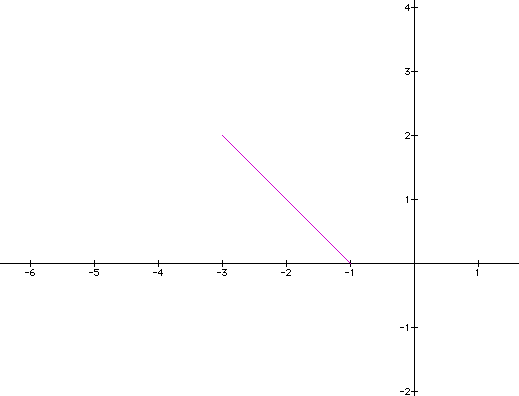
We see that the graph has a slope of -1 and passes through the point (-2,1) as predicted.
If we let k = -3 and graph the equation over the first one, we get the following equations and graph:
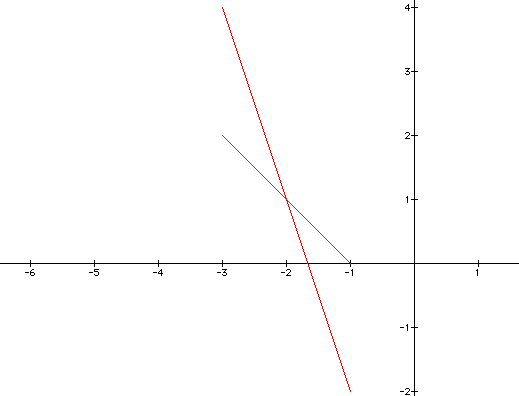
We see that the graph has a slope of -3 and passes through the point (-2,1) as predicted.
And finally, if we let k = 2 and graph the equation over the first two, we get the following equations and graph:
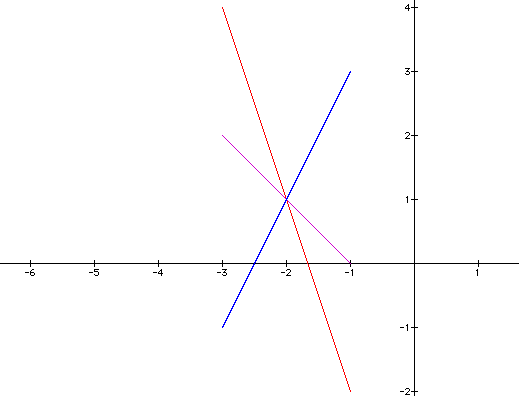
We see that the graph has a slope of 2 and passes through the point (-2,1) as predicted.