Investigate the following equations with different values of p:
for k > 1.
We will start by examining the graphs when k = 1.4 and p is varied.
If we let p = 1 in the first equation, we get the following equation and graph:
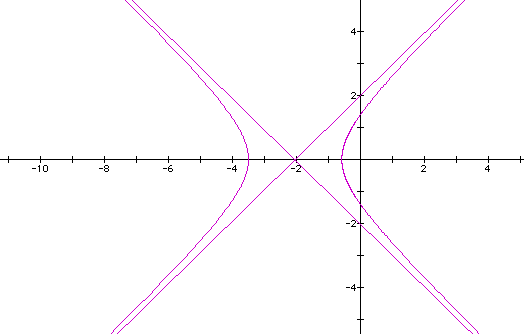
which is a hyperbola.
If we let p = 2 and graph this equation on top of the first one, we get the following equation and graph:
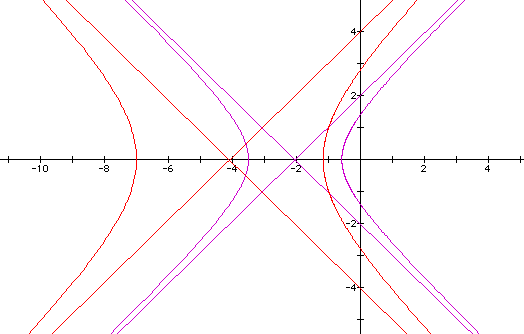
By letting p = 2, we have essentially doubled the radius at each point which has the effect of "spreading out" our curve.
If we now let p = 0.5, we would expect to half the radius at each point of our original graph. This would have the effect of "pulling in" or shrinking our curve. The equation and graph, laid over the original, are as follows:
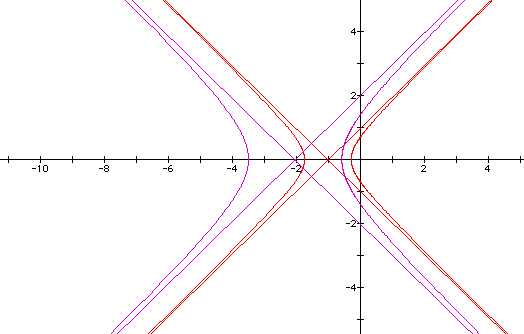
We can see that we obtained the expected results.
We will now look at negative values of p. If we make p negative, we are essentially multiplying the radius by -1 at each point. This should have the effect of reversing the direction of the radius from the origin. The length of the radius should remain unchanged. We should see a reflection of the graph through the origin.
We will look at our original equation again.
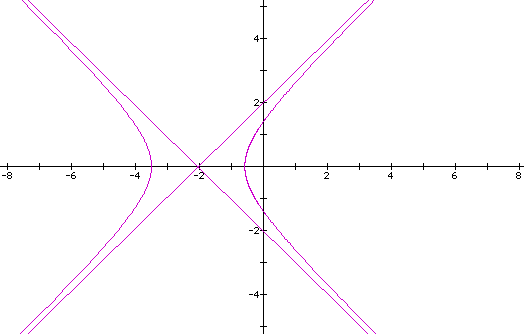
If we now let p = -1 and lay this graph over the original, we get the following:
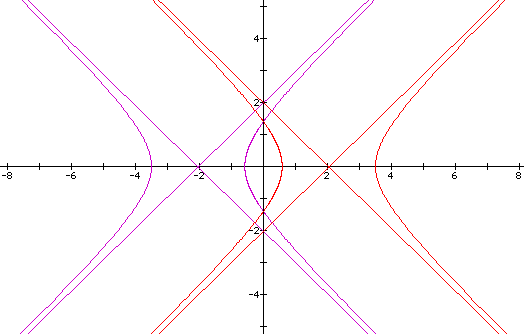
We can see that we obtained the expected results.
If we let p = 1 in the second equation, we get the following equation and graph:
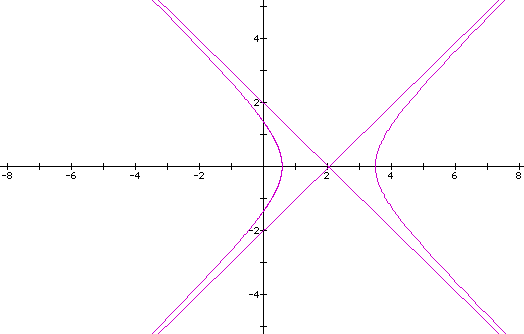
which is a hyperbola reflected across the y-axis from the first equation. Varying p will have the same effect on this graph as it did on the first.
If we let p = 1 in the third equation, we get the following equation and graph:
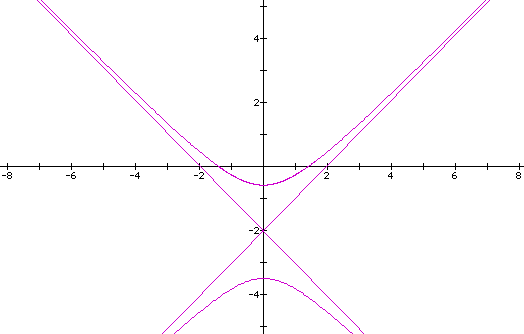
which, again, is a hyperbola. Varying p will have the same effects as above.
And finally, if we let p = 1 in the fourth equation, we get the following equation and graph:
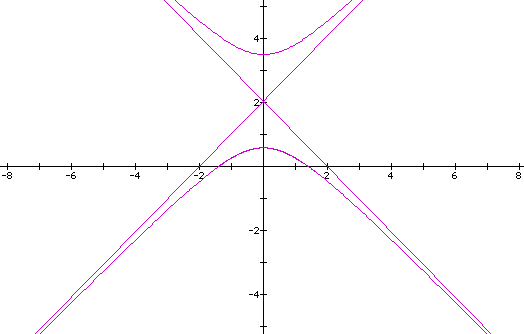
which is a hyperbola reflected across the x-axis from the third equation. And again, varying p will produce the same effects as above.
Click here to see a graph as k is varied from 1 to 4 in the first equation.
To examine the graphs when k < 1 and p is varied, click here.