

To start this problem, we draw a picture to help visualize it.
First, we have a 5x8 sheet of paper.
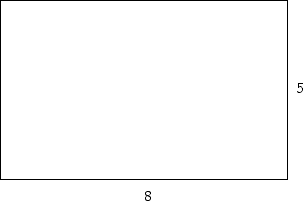
Next, we cut squares out of the corners so that what is left can be folded up into the shape of a box. The following drawing shows the squares cut out and the fold lines for the box.
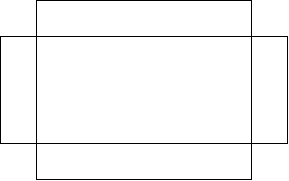
We can see that altering the size of the squares we cut out will affect the shape and volume of our box. Our problem is to figure out what size cutout results in the largest possible volume.
If we call the length of a cutout square x, then we can label the drawing as follows.
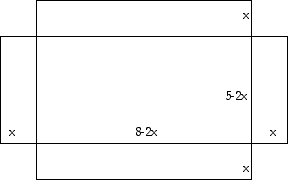
If we fold up our box, we can see that the length will be 8-2x, the width will be 5-2x, and the height will be x.
This gives us a formula for finding the volume of our box:
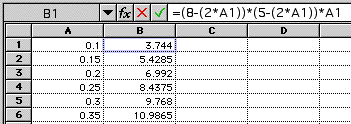
We can now set up a spreadsheet to calculate the volume for various values of x.
We set up column A for different values of x. The values range from 0.1 to2.5. We do not have to go past 2.5 since the width of our sheet is only 5 and two squares of 2.5 each would use up the whole width. We use increments of 0.05 so we will have plenty of data points. Column B is used for the volume formula. Below we see a picture of the first six rows and the volume formula.
Click here to see the entire spreadsheet.
We can now make a graph of the data. Making a scatter plot of the data produces the following graph.
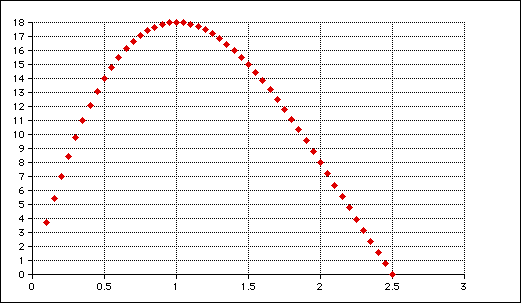
The size of the squares is shown along the x-axis and the volume of the box is shown along the y-axis.
From the graph we can estimate the maximum volume of the box to be 18. This value occurs when the size of the squares cut out of the corners is 1x1. Thus, the dimensions of the box are 6x3x1.
If we wanted more accuracy, we could look at a much smaller range of numbers with 1 somewhere in the middle of the range. We would also need to reduce the increments between numbers. If the increments get to small, however, we will exceed our ability to measure accurately and actually build the box.