

Prove that the three perpendicular bisectors of the sides of a triangle are concurrent.
Take a triangle ABD where lines EH and FI are perpendicular bisectors of segments AD and AB respectively and G is the midpoint of segment BD. Line EH intersects segment AD at E and line FI intersects segment AB at F. Since segments AD and AB intersect, we know that lines EH and FI must intersect since they are perpendiculars of those segments. We will call the intersection C.
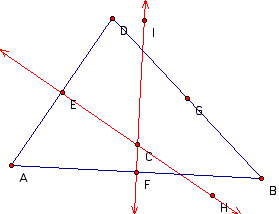
We now draw segments AC, BC, and DC and remind ourselves that segments EC and FC are perpendicular bisectors of segments AD and AB respectively.
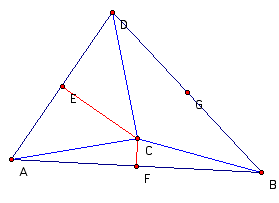
Next we will look at triangles AFC and BFC. We know that segment AF is congruent to segment BF since F is the midpoint of segment AB. We know that segment FC is congruent to itself. And since segment FC is perpendicular to segment AB, we know that angles AFC and BFC are right angles and therefore congruent to each other. Therefore, by the SAS theorem, triangles AFC and BFC are congruent to each other.
We can now conclude that segment AC is congruent to segment BC since corresponding parts of congruent triangles are congruent.
By a similar argument, we can see that segment AC is congruent to segment DC.
And since segment BC is congruent to segment AC and segment AC is congruent to segment DC, we have that segment BC is congruent to segment DC.
Now we will look at triangle BCD. First, we will draw segment GC.
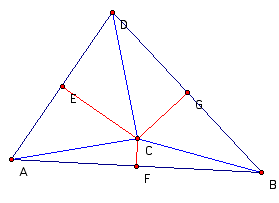
We showed above that segments BC and DC are congruent. We know that segments BG and DG are congruent because G is the midpoint of segment BD. We know that segment GC is congruent to itself. And so by the SSS theorem, triangles BGC and DGC are congruent to each other.
Now we know that angle CGD is congruent to angle CGB since corresponding parts of congruent triangles are congruent. Since segment BD forms an angle of 180 degrees, it is clear that angles CGD and CGB both measure 90 degrees and are therefore right angles. Since segment CG forms right angles with segment BD and bisects segment BD at G, we conclude that segment CG is the perpendicular bisector of segment BD.
We remember that segments EC and FC are the perpendicular bisectors of segments AD and AB, and that they intersect at C. We have shown that segment GC is the perpendicular bisector of segment BD and that it also intersects C.
Therefore, we conclude that the three perpendicular bisectors of the sides of a triangle are concurrent.