

I will examine the construction of the common tangents to two given circles. I do not intend for this to be a proof, but more of a how-to.
I started with two circles that were separate. That is, they did not intersect nor was one contained in the other.
I could see that there would be four tangent lines. One would go across the top of the two circles. One would go across the bottom. The two others would cross in between.
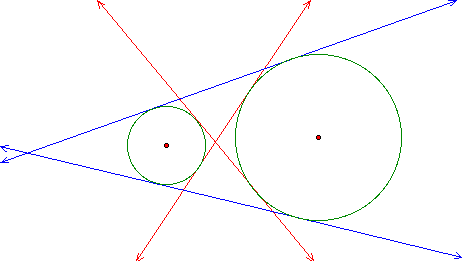
Click here to see how to find the outer tangents.
Click here to see how to find the inner tangents.
Click here to see a tool for finding the tangents to two circles.
Use the tool to see what happens when the circles intersect or when one circle is contained within the other.