

Given a line and a circle with center K. Take an arbitrary point P on the circle. Construct two circles tangent to the given circle at P and tangent to the line.
It would be helpful to look at a sketch of the completed problem.
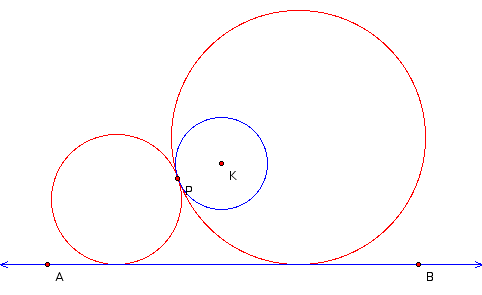
The key to this problem is locating the centers of the two tangent circles. If we can locate the centers, then we can simply construct the circles using point P for each radius.
We can see from the first sketch that the finished construction will have three circles. They will all be tangent to each other at the point P. We know that the centers of tangent circles lie on a line through the point of tangency and so our first step is to construct that line. If we draw a line through point K and point P, then we know the centers of the tangent circles will lie on that line.
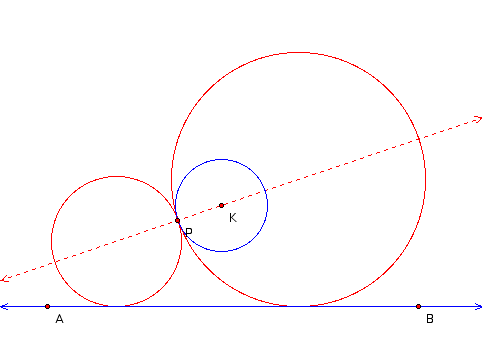
We also know that if we draw a line through point P that is perpendicular to line PK, then that line will also be tangent to our three circles at point P.
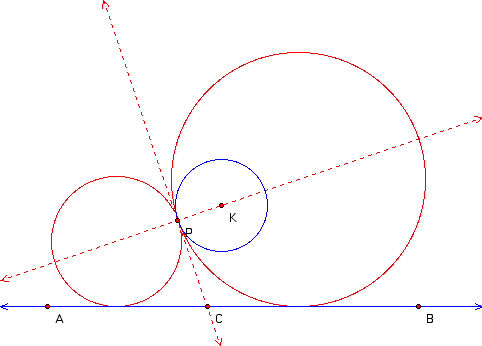
By drawing line PC, we have created angle ACP. We know that the smaller circle is tangent to line PC and line AC. And so we have a circle inscribed in an angle. We know that the center of a circle inscribed in an angle lies along the angle bisector. Therefore, the center of the smaller circle lies on the bisector of angle ACP. A similar argument for the larger circle will show that its center lies on the bisector of angle BCP. We now draw the angle bisectors.
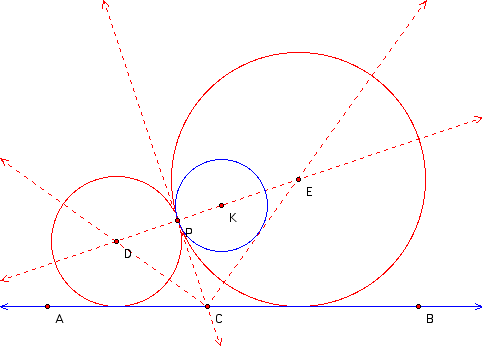
The bisectors of angle ACP and angle BCP intersect line PK at point D and point E respectively. Since the angle bisectors contain the centers of our circles and we already know that line PK contains the centers of our circles, we can conclude that the intersections of the angle bisectors with line PK must be the centers of our circles. And so we have point D and point E as the centers of the two tangent circles.
Click here for a GSP sketch to explore.