

Given triangle ABC and its circumcircle. Show that there is a point P on the circumcircle such that side AC is its Simson line.
First, we draw the given triangle and its circumcircle.
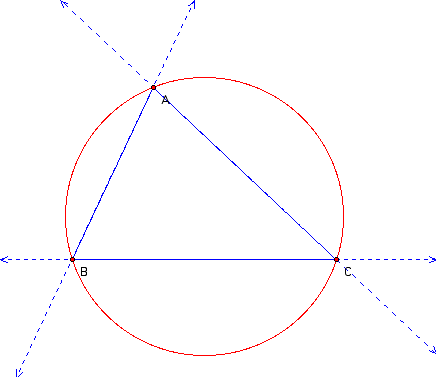
Next, we construct the perpendicular to line AB at point A. We label its intersection with the circumcircle point P.
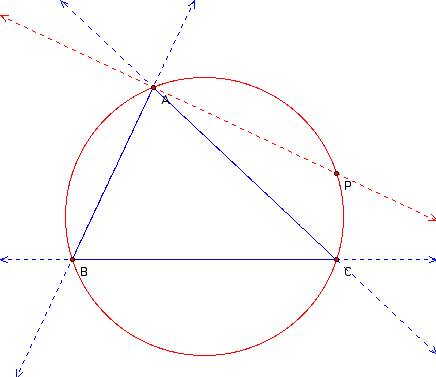
Next, we draw line BP.
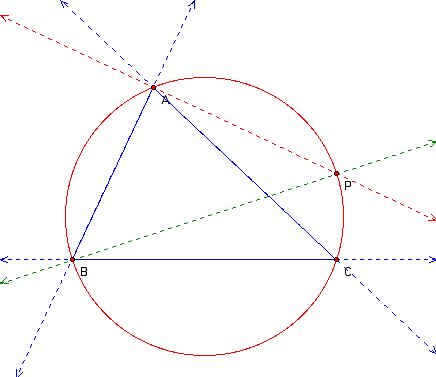
Since points B, A, and P lie on the circumcircle and angle BAP is a right angle, we know that line BP is a diameter since a right angle inscribed in a circle intercepts the circle at a diameter.
Next, we draw line CP.
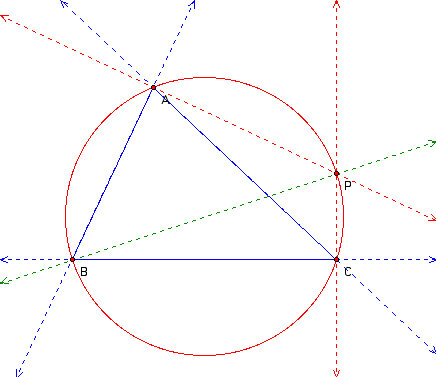
Since angle BCP is an inscribed angle that intercepts a diameter, we know that it is a right angle. Therefore, line CP is perpendicular to line BC at point C.
Next, we construct the perpendicular to line AC through point P. We label its intersection with line AC point D.
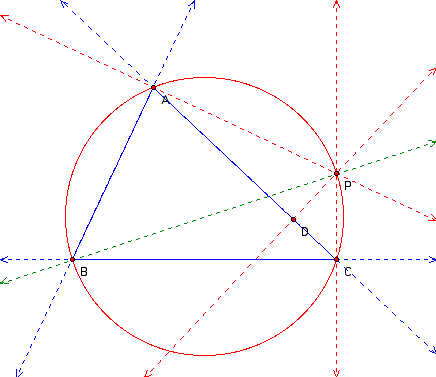
We have shown that line AP is perpendicular to line AB at point A and that line CP is perpendicular to line BC at point C and that line DP is perpendicular to line AC at point D. Therefore, point P is a pedal point of triangle ABC.
Line AC contains the points A, C, and D ( i.e. the points of intersection of the perpendiculars from P ) and is therefore the Simson line.
We have shown that there is a point P on the circumcircle such that side AC is its Simson line. We have also shown that point P lies on the diameter of the circumcircle that passes through point B.
Similar proofs will show that point P can be located such that the Simson line coincides with side AB or side BC.