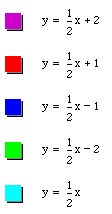
Objectives:
1. to know the definition of parallel lines
2. to be able to write the equation of a line parallel to a given line
3. to understand and explain what makes lines paralles and their characteristics
Definition:
Parallel Lines: lines that have the same slope. These lines will never intersect.
Parallel lines are lines that never intersect because they have the same slope (m). So, this means that they only possible difference in there equations is the y-intercept (b). That makes it very easy to tell it lines are parallel given their equations in slope-intercept form. To me, it much easier to tell this than by looking at their diagrams.
Here are a few examples of parallel lines. Notice, that the slope is the same in all of the equations.
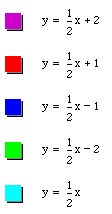
The slope in each equation is one-half, but each equation has a different y-intercept. The y-interecepts range from -2 to 2. This means that if we would look at their graphs, they should never intersect. The graphs below illustrate this point.
Example1: Are the following pairs of lines parallel?
a)
. No, because their slopes are different. This can also be seen graphically by:
Notice, that the lines intersect on the graph. Would the lines be parallel if they are the same line? No, if they are the same line then one doesn't have two lines which we need to have parallel lines.
b)
. Yes, they have the same slope because the slope of the top equation reduces to be the same as the slope of the bottom equation. Remember to make sure that they slopes of the lines are simplified before deciding whether or not lines are parallel. It can also be seen graphically that they are parallel.
For any given line, how many differnent lines are there that are parallel to the given line? Infinite because there are an infinite amount numbers that can be used as the y-intercept. Click here to start a movie that will help to convince of that fact.
Note: A word of caution. It is not a good idea to rely on graphs to determine if lines are parallel. It is possible to draw lines whose slopes are so close to one another that it is practically impossible to tell that they are not parallel by just looking at them. To illustrate this point look at the next graph and decide if the lines are parallel.
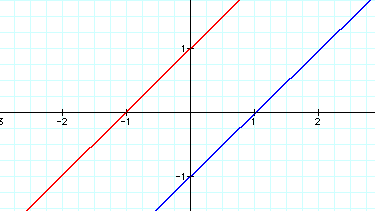
To me, these lines look parallel, but they are actually not because the equations of the lines are:
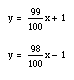
These equations are very similar but since their slopes are different, they will eventually intersect.
Now that we understand what makes lines parallel and how to tell if lines are parallel, we want to be able to actually write the equations instead of being given the equations. For this, we will again use the the slope-intercept form from day 5 and the point-slope form from day 7.
For these problems, we will be given the equation of a line and asked to write the equation of the line that is parallel to the given line through a particular point. Examples 2 and 3 will illustrate how this is done.
Example2: Write the equation of a line that passes through the point (0, 5) and is parallel to:
Step 1: Determine the slope of the new line.
The new line must have the same slope of the old line so m =
.
Step 2: Choose between slope-intercept form and point-slope form.
In both cases we neeed slope, so that does not help us with our decision. So, we look to the given point. If the point tells us the y-intercept, we use slope-intercept form; if it doesn't, we use point-slope form.
In this case, the point (0, 4) tells us that b = 4. That means we should use slope-intercept form (y = mx + b). Now, make the substitutions for m and b to get:
which is the equation of the desired parallel line. Graphically, the situation looks like:
Example3: Write the equation of the line through the point (-2, 1) parallel to the line:
Step 1: Determine the slope of the new line.
The slope of the parallel line is
.
Step 2: Choose between slope-intercept form and point-slope form.
In this case, we the point does not tell us what b is so we will have to use point-slope form, y - y1 = m(x - x1).
Next, Substitute in: m =
, y1 = 1, and x1 = -2.
This gives us the equation:
.
Distribute to get:
.
Solve for y to find the equation of the parallel line to be:
.
Just as a check to see if they are parallel, we graph the two equations to get:
.
We should now be able to determine is lines are parallel, and write the equations of parallel lines.