By this point in time, we have solved first degree equations for years. We did this in elementary school when teachers asked us questions like three times what number plus one is ten. Here, mental math was usually used to find the number to be three.
Later, we learned how to represent this algebraically. This then gave us the equation 3x+1=10. We then learned how solve for x by isolating the variable. Here, we would first subract 1 from both sides to get the equation 3x = 9. Then, we divide both sides by 3 to get the answer of x = 3.
But, why does this work? Is there another way to find the answer x = 3?
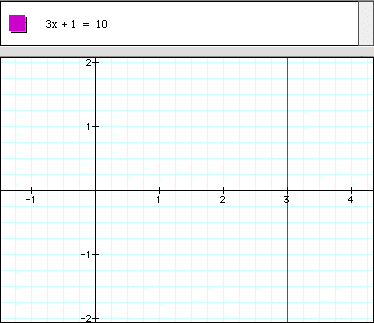
Another possible way to find the answers to this is to look at the graph of the equation. What do you think that it will be?

Are you surprised that it is a vertical line at x= 3? You shouldn't be because that is what we already said the answer was. Remember, that one gets a vertical line when the equation is of the form x = some number. Therefore, the answer to the equation occurs at the point where the graph, in this case a vertical line, intersects the x-axis. So, the answer to the equation is 3.
So, what is the point of this? Why does one spend time graphing a simple first degree equation like this? To make connections between different aspects of mathematics and what they are telling us.
What are the connections in this case? Hopefully, we now realize that the graph of first degree equations are linear and that the solution to the equation occurs at the x-intercept. Or, whatever variable you choose to use. So, if one wanted to solve an equation in terms of y-graphically one would need to find the y-intercept.
What is the solution to the equation: 2y + 5 = 17?
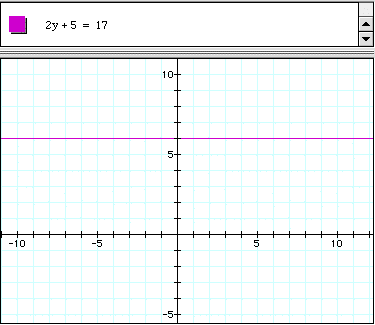
Based on the graph, the answer is 6. So, let's check the answer does 2(6) + 5 = 17. Yes, so we found the answer graphically without ever having to use algebraic manipulation.
What would one do if the variable in the equation was something other than x or y? Simple, the variable name does not matter. So, just change the variable to x or y.
Now that you have a better understanding of where the solution to simple one-variable, first degree equations. It is time to solve them using algebraic manipulation.