First, a quick reminder of what a quadratic equation is. A quadratic equation is an equation whose largest exponent is two, or in other words, a second degree equation. When graphed, second degree equations are parabolic in nature. The general form is :
There are several methods for solving quadratic equations: factoring, completing the square, the quadratic equation, and graphing. We looked in depth at the first three in Algebra I and will review those concepts again shortly in Algebra II. But, we did not spend any time looking at why these concepts work. They work because the solutions to a quadratic equation are the point(s), if any, where the graph intersects the x-axis. So, all that factoring, completing the square, and the quadratic formula do is give us an algebraic method for finding the x-intercepts. These methods are very useful for finding the exact answers, but thanks to technology we can once again use graphing methods to find the solution.
This is due to the fact that graphing with pencil and paper is very in precise especially when the graph is non-linear. Thanks to technology however, we are able to get very precise graphs of non-linear functions. So, we will look at how to use technology to find the solutions to quadratic equations.
Based on the fact that we are looking at second degree equations, we expect to find two answers to ever y equation. This however is not always the case. There are cases where the number of answers is only 1 (a double root) and also when there aren't any answers. So, we must remember that our possible number of solution are: 2, 1 or no solution.
Take the equation:
We could factor this into (x + 1)(x + 3) = 0 and solve it to find the answers to be x = -1 and -3. Now, let'g graph this, find the x-intercepts of the graph and see if they are -1 and -3.
To use the Ti-83 to graph the equation, do the following:
Step 1: Hit the Y= button. If you have any equations currently typed in, clear the equations.
Step 2: Type in our equation. In the calculator, the equation will look like:
x^2 + 4x + 3 Step 3: Hit the graph key. You should now see graph that looks like the following.
Step 4: Move your cursor to the points of intersection. The should be -1 and -3.
Your graph should look like:
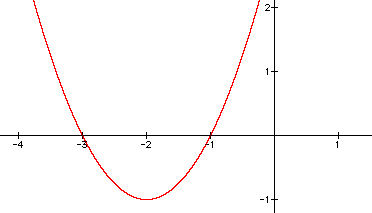
It does have x-intercepts of -1 and -3.
Take the equation:
To solve this, we would just take the square root of both sides and find the answer to be 0. This is a double root, so we get only one answer. Now, type this equation into your TI-83 and see if the graph gives the same answer. Your graph should look like:
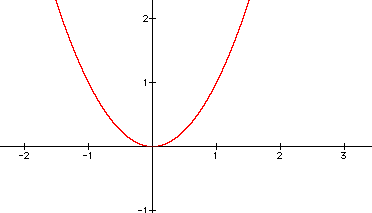
Take the equation:
To solve this equation we would first subract four from each side to get:
Then, we would take the square root of both sides and have:
The square root of -4 does not have any real number solution. Therefore, there are no solutions (x-intercepts) for x. Now, graph the equation in your calculator to check the answer. The graph below shows that there are no x-intercepts, thus the quadratic has no solutions.
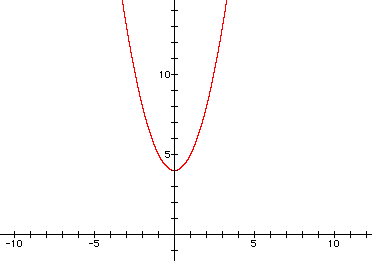
Use your graphing calculator to solve each of the following quadratic equations for x.
1.
2.
3.
4.
5.
Click here to see the Solutions