Logarithmic functions are used to find unknown exponts. Take the following equation for example:
In order to solve this, we need an inverse operation to an exponent which is a logarithim. This cannot be done in or head, but we should have some idea of the answer. We know that 10 to the first power is 10, and that 10 to the second power is 100. This means that x must be between 1 and 2. Since 85 is very close to 100, that tells us that the answer should be close to 2 so maybe 1.8.
Current technology would allow us to quickly determine values
for 
in order to determine
a good approximation for the desired decimal. However, this would
be time consuming. So, we need a way to find the true value. This
method is logarithms.
In order to solve this basic equation all we must do is use the log key on our calculator and find the log of 85 which is 1.9294.
Every exponential equation has an equivalent logarithmic equation. So, for any positive base b, where b does not equal 1:
if and
only if x = logby For Example:
Given the exponential equation:
we can write an equivalent equation in logarithmic form. First, the exponent is the x, what it equals is y, and the base is b. This gives us 3 = log5125.
We can also go from a logarithmic equation to an exponential equation. For example:
4 = log381. This equation tells us that 3 to the fourth power is 81. Which written as an equation would be:
.
Now that, we understand the equivalent forms, it is time to look at how to solve different types of logarithmic equations.
Solving logarthimic equations is based on the fact that every
expontial function has a logarthmic function that is its inverse.
Given the logarithmic equation, y = logbx,
its inverse is 
. These
are symmetric about the line y = x. Take the following equations
for example:
y = log10x and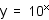 
We will graph them along with the line y = x to demonstrate that they inverses symmetric to the line y = x.
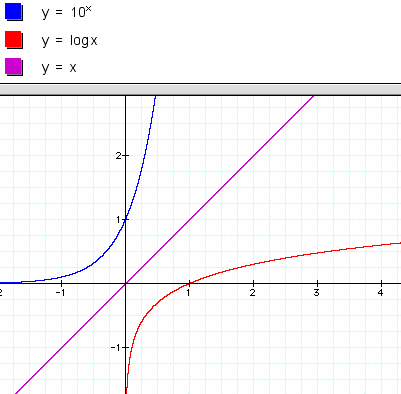
Now that we have demonstrated the fact that every logarithmic function has an exponential function which is its inverse and vice versa. We want to be able to solve logarithmic functions. This ability to solve comes from the One-to-One property of exponents.
The One-to-One property of exponents states that for any base b and exponents x and y, if b to the x equals b to the y then x must equal y. This could also be written as:
= 
then x = y.This fact allows us to solve logarithmic equations by transforming them into their equivalent exponential equations with equivalent bases. Then, all that is left to do is to set the exponents equal to one another and solve for the variable.
For example:
Suppose we want to solve the following equation for y.
y = log1255 First, we would turn this into its equivalent exponential form which is:
Now that we have an exponential equation, we both sides to have the same base. So, we need to rewrite 125 as 5 to the third power.
This equation can be written as:
Now that the bases are the same, we use the One-to-One property of exponents to set the exponets equal. This means that
3y = 1 Finally, we solve for y by dividing both sides by 3. This means that
A second type of logarithmic equation that we need to be able to solve is when the base is unknown. This would take a form like the following example.
5 = logx32 Here again, we start by turning the logarithmic equation into its equivalent exponential equation.
When we are solving for the base, we need to have equivalent exponents instead of equivalent bases. So, here we need to change 32 into 2 to the fifth power.
Now that they have the same exponents, to be equal they must have the same base so:
.
Is there another way to solve this? Can you use your TI-83 to solve the equation
What if we did the inverse operation of the fifth power to each side? This would mean taking the fifth root of each side or taking each side to the one-fifth power. Again, we would find that x=2. So, we can use technology to speed up the process once we have changed the equation into exponential form.
The third and final form of logarithmic equations that we are going to solve are those where the x is unknown. This will take the form similar to the following example.
4 = log3x Again, we start by rewriting the equation into exponential form.
Now all that is left to do is find the value of 3 to the fourth power which is 81. Thus,
This concludes our look at logarithmic functions. Now, we should be able to write them in equivalent forms and solve any of the three types discussed above.
