This write-up will involve forms of the equation:
where n is a natural number greater than 1.
The graphs of this equation form two distinct patterns. The first pattern is for when n is even and the second pattern when n is odd.
The first case to look at is when n=2. By substitution, that
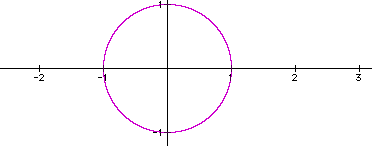
gives the equation 
which
is the equation of a circle with a radius of 1. The graph of this
equation is below.
As n increases, the graph starts to change shape. Instead of
a circle, it starts to look like a square with rounded corners.
This can be seen in the graphs of the following equations: 
(red),
(purple),
(blue).
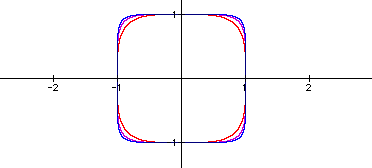
As can be seeen by the graphs, as n increases the graphs look
more and more like a square with sides of 1 unit. Now, what would
the picture look like when n=24? Will it look like a square or
will the corners still appear to be rounded? If they still appear
to be rounded, when will the graph look like a square or will
the rounded courners ever go away? Let's predict that the graph
will still have rounded corners. Now, let's look at the graph
of 
.
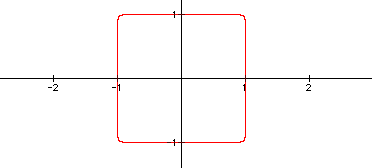
The graph shows the prediction to be correct that the corners
are still rounded. Now, use graphing calculator to make the graphs
of 
. This allows the
program to run make the graph of any value of n. Doing this allows
us to see that when n = 90 the graph does appear to be a square.
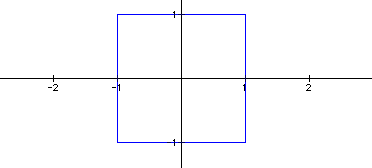
When n=odd integer greater than 1, the pattern is completely
different. From the graphs above, one would think that these graphs
would also be either circular or polygonal. This is not the case
as can be seen when by the graph of 
.
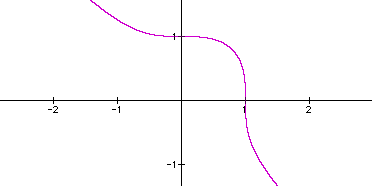
This graph does not come back to itself as the graphs of the
first case did. This graph has tails, curvature between x=0 and
x=1, and it appears that there is an asymptote. Now, the question
becomes what happens to this graph as n increases. In order to
get some idea, we will look at the following cases in order to
make a prediction: 
(purple),
red,
(blue).
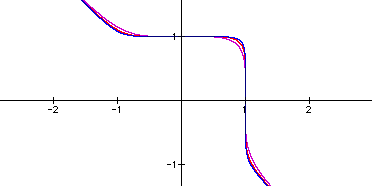
From the above graphs, it appears that as n increases that the curvature of the graph between x=0 and x=1 decreases. That would lead to the prediction that as n increases the curve would go more and more towards a corner instead of a curve. So now, let's see find the graph of the equation when n=25.
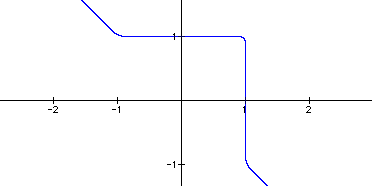
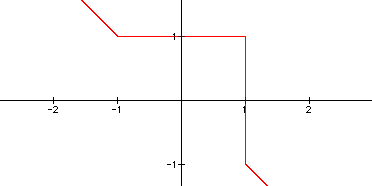
As predicted, the curvature has again decreased. Now, one wonders
if the corner appears to form a right angle when n is around 90
as it does in the even case. Which it appears to do when looking
at the graph of 
which
is below.
Click here for a movie of .