Write-up #2:
The graphs of the equation 
are
parabolas that will either open upwards or downwards. The coefficient
a will make translations to the basic graph of a parababola which
is 
and whose graph
is below.
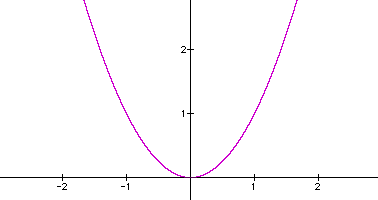
There are two basic patterns to explore for these parabolas. The first is when a is a positive real number and the second is when a is a negative real number. There is no reason to look at the scenario when a=0 because that would just give the point (0,0). Now, let's explore what happens when a is a positive real number.
This scenario needs to be broken into two parts. The first part is when 0<a<1 and the second part is when a>1. Recall that we have already looked at what happens when a=1 and that all of the transformations are based on that parabola.
So, when 0<a<1, what happens to the parabola. Does it
move up or down? left or right? Is it expanded or maybe shrunk?
To help understand the pattern, start by making some graphs that
would lie in this range. Below are the graphs of 
(purple),
(red), 
(blue),
(green).
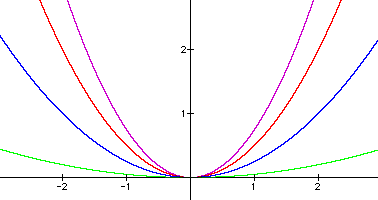
The graphs show a distinct pattern that can be generalized for this scenario. When a is a real number between 0 and 1 non-inclusive, the distance between the sides of the parabola increases, or the parabola expands. This would also be thought of as a horizontal stretch, or if one prefers an analogy, this is when the dentist says, "Open wide."
A mathmatical way of explaining the scenario would be: if a
is a real number between 0 and 1 non-inclusive the graph of the
equation undergoes a horizontal
expansion. The expansion increases as a approaches zero or in
other words, as a decreases the expansion increases. Thus, a and
the expansion are inversely related.
Now, what if a>1? Does the graph still expand? To see what
happens here, again use the graphing calculator to see what happens
for different values of a. Below are the graphs of: 
(purple),
(red), 
(blue),
(green).
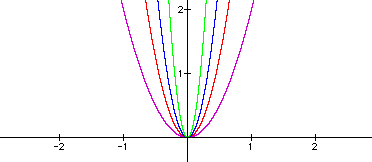
The graphs show a distint pattern. As a increases the distance between the sides of the graphs decreases or contracts. An anology for this would be to close a mouth. This would be a horizontal contraction. Thus, for a>1, a and the contraction are inversely related.
The a = negative real number scenario is analagous to the a
= positive real number scenario. The only difference between the
two is that the negative sign inverts the graphs or if one prefers,
it flips the graphs over. This can be seen on the following graph
which has 
in red and 
in blue.
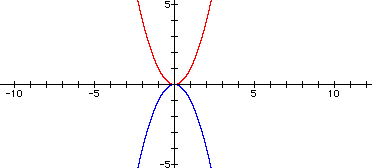
There are still two scenarios to explore. The first is when
-1<a<o. This range expands the graph just like when 0<a<1.
The graphs of 
(purple), 
(red), 
(blue),
and 
(green) are below.
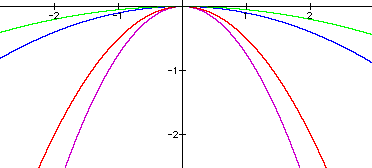
The second scenario is when a<-1. This range contracts the
graph just like when a>1. The graphs of 
(purple),
(red), 
(blue),
and
(green) are below.
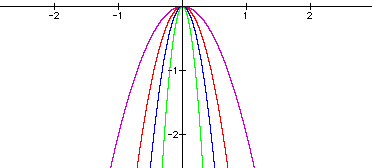
Now, one understands how the coefficient of an 
affects
the graph of the parabola.