
Write-Up #4:

The relationship between N (the center of the nine point circle), G(the centroid of the circle), H(the orthocenter of the circle) and C (the circumcenter of the triangle) is that they are all collinear no matter the shape of the triangle. Below is a picture with N, G, H, C, and the nine point circle. This will be used to explore the above claim and to convince the reader that it is true.
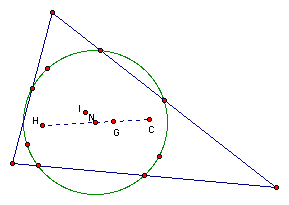
In order to show that the claim is true, we will look at N, G, H, and C in an acute triangle, a right triangle, an obtuse triangle, a scalene triangle, an isosceles triangle, and an equilateral triangle.
The above picture is both acute and scalene. In this case, the points N, G, H, and C are collinear as claimed.
The next picture is that of a right triangle.
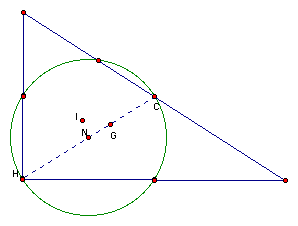
Again as claimed, the points N, G, H, and C are collinear. Now, let's look at the picture of an obtuse triangle.
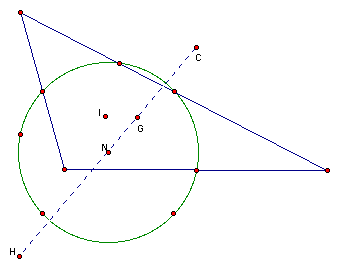
Again, the picture supports the claim. So, now it is time to try an isosceles triangle.
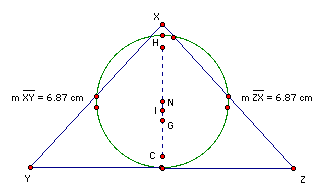
Just as before, the picture supports the claim. Notice, that in this case, I is also collinear. Finally, it is time to try an equilateral triangle.
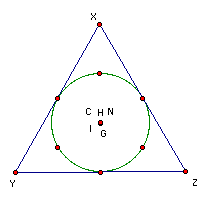
This picture is a different from the rest. Here, all of the points converge to become the same point. This gives a specail case and supports the claim because a point is on any line that could be drawn. So again, N, G, H, and C are collinear. Notice, that in this case I has also converged to the point.
By looking at the different types of triangles, it appears that the claim of N, G, C, and H being collinear is true. Note: This use of GSP is by no means a proof. It is just a tool that allows us to easily look at the differnent scenarios.
If you have GSP 4.0 installed on your computer, click here for an interactive diagram.