

This construction starts with two given circles. It does not matter if one circle is inside the other, or if the circles intersect, or if the circles are disjoint. The construction will work for all three cases. To me, it is easier to see the construction for the situation when on circle is in the interior of the other and that is what the construction that will be presented here. This is done because GSP allows the user to move the cirlces into any position and the construction still holds. Note: if you want to make a tool in GSP, the given circles should be constructed from two points not from the circle tool.
So, start with two circles and an arbitrary point(A) on one of the circles.
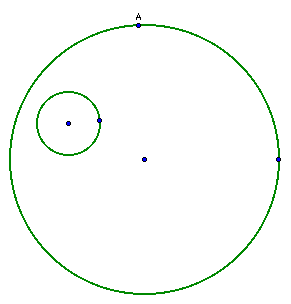
Next, construct the line through the center of the the large circle and A. Also, constuct the radius of the small circle. Now the construction should look like this.

We now need to constuct another circle with radius equal to the length of the small circle with its center at point A and find the point B where this new circle intersects the line.
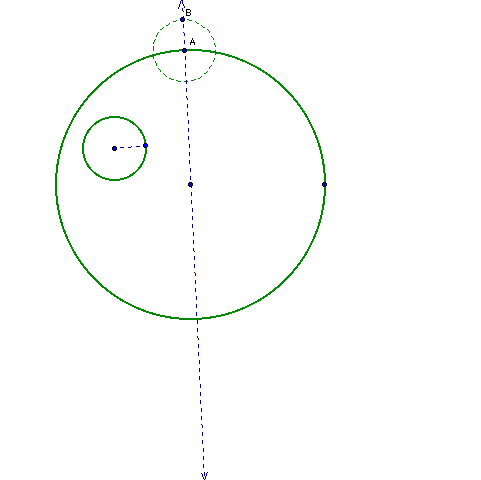
Next, constuct the segement from point B to the center of the small circle. This gives us the base of the isosceles triangle that the construction is dependent upon. While we are at it, find the midpoint of the segment and the line perpendicular to the segment at the midpoint.

The last two steps of the constuction are two find the point where the two lines intersect which is the center of the circle tangent to the two given circles. Now, use the newly found point and point A to constuct a circle and this circle will be tangent to the two given circles.

Click here for a GSP sketch and tool of the above construction.
Another interesting construction is the circle tangent to the given circle on the interior and the tangent circle. Click here for a GSP sketch and tool of the constuction. A picture of the constuction is below.
