
Write-Up #8:

This discussion starts with a given triangle ABC and its orthocenter H. The orthocenter was found by using the tool/script from write-up 5. So, our basic picture looks like this.
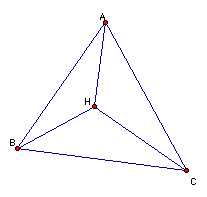
There are now four triangles, ABC, ABH, BHC, and ACH. It is now possible to construct the nine-point circle for each of these triangles. One would guess that since there are four different triangles that there would be four differnt nine-point circles. This however is not the case. When one constructs the nine-point circles for the four triangles, they are all the same circle. See the picture below for an illustration of this.
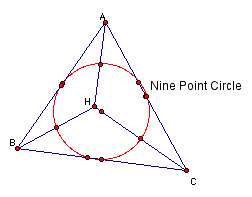
Based on this example, one could make the conjecture that the nine point circle is always the same for the four triangles.
Click here for a GSP sketch that will all you to move the vertices of the triangle. These movements will help to convince you that the conjecture is correct although it does not prove the conjecture.
First of all, remember that the nine-point circle is composed of the the three midpoints of the sides, the three feet of the altitudes, and the three midpoints of the segments from the verticies to the orthocenter.
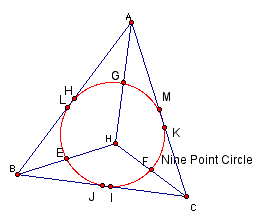
Notes:
1. For triangles ABH, ACH, and BCH, the missing vertex of triangle ABC is the orthocenter.
2. The altitudes for all of the triangles are the same so the points L, I, K which are the three feet of the altitudes should be in all four nine-point circles.
3. E, F, G, H, M, J are the midpoints of the segments that they lie upon.
From note 2, we already have 3 of the nine points. The points E, F and G are the midpoints of the segments from the vertices of triangle ABC to the orthocenter. So, they should be on triangle ABC's nine-point circle. Finally, H,J, and M are the midpoints of the sides of the triangle. So, the points E, F, G, H, I, J, K, L, and M are the points on the nine-point circle for triangle ABC.
From note 2, we already have 3 of the nine points. The points E, G, and H are the midpoints of the sides of the triangle so they are on the nine-point circle. For this triangle, H is the orthocenter. The points J, F, and M are the midpoints of the segments that connect the verticies to the orthocenter. So, the points E, F, G, H, I, J, K, L, and M are the points on the nine-point circle for triangle ABC.
From note 2, we already have 3 of the nine points. The points M, G, and F are the midpoints of the sides of the triangle so they are on the nine-point circle. For this triangle, B is the orthocenter. The points J, H, and E are the midpoints of the segments that connect the verticies to the orthocenter. So, the points E, F, G, H, I, J, K, L, and M are the points on the nine-point circle for triangle ABC.
From note 2, we already have 3 of the nine points. The points E, F, and I are the midpoints of the sides of the triangle so they are on the nine-point circle. For this triangle, A is the orthocenter. The points G, H, and M are the midpoints of the segments that connect the verticies to the orthocenter. So, the points E, F, G, H, I, J, K, L, and M are the points on the nine-point circle for triangle ABC.
We have now shown the points E, F, G, H, I, J, K, L, and M are the points on the nine-point circle for each of the four triangles. Since each of the four nine-point circles have the same points, the four nine-point circles must be the same circle. This proves that the conjecture is correct.