
Write-Up #9:

This contruction starts with a circle and a point chosen at random on the circle that will be used as the pedal point of a triangle. The triangle is then constucted within the cirlce and the contrcution now looks like this.
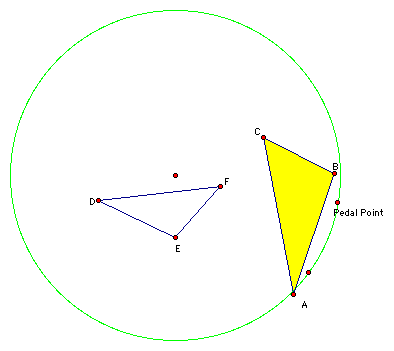
Next, the pedal triangle(triangle ABC) of triangle DEF is constructed using the point labeled as Pedal Point on the circle as the pedal point. So, the next step in the construction looks like the following.
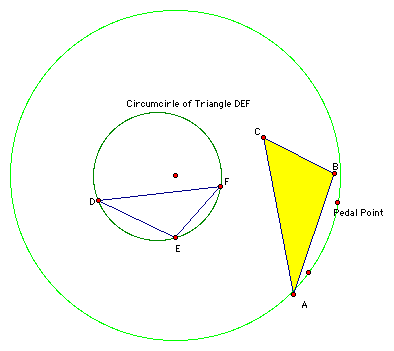
We can now find the circumcircle of triangle DEF just to check and make sure that the radius of the original circle is larger than the radius of the the circumcircle.
Since the radius of the triangle is larger than the radius of the circumcirle, we now find the midpoints (X, Y, Z) of the sides of the pedal triangle ABC.
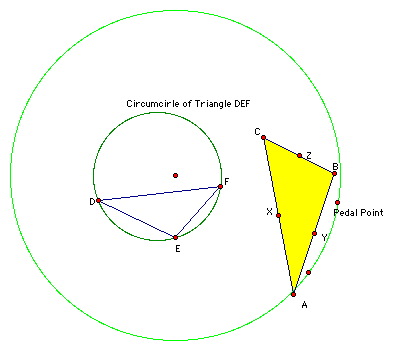
Finally, it is time to make a conjecture about the loci of the points X, Y, and Z as the Pedal Point is animated around the the original circle. Will it be circular? Elliptical? Triangular? A different shape? Or Random?
Two ways to determine the loci of the midpoints, X, Y and Z are the following. First, GSP has a locus command that will create the locus of the midpoints. Second, the midpoints could be traced as the Pedal Point is animated around the original circle. Either way will result in the same loci which are ellipses. The sketch of the loci are below.
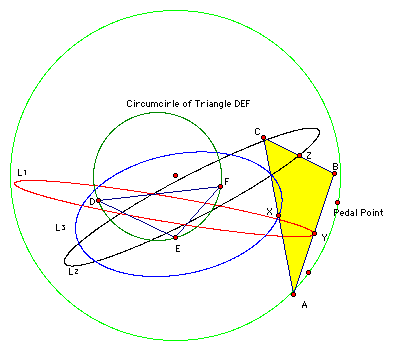
Click here for a GSP sketch of the the picture above that has an animation button to trace the loci and the loci constructed using the the locus command.