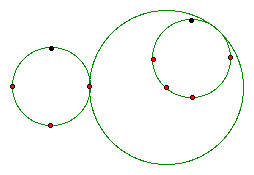
Suppose that one is given a circle with two circles tangent to the given circle. One of the circles is tangent on the interior of the circle and the other circle is tangent on the exterior of the circle. The tangent circles have a radius that is proportional to the radius of the original circle. A picture of this could look like the following.

The question becomes how many revolutions will either of the small circles make if it rotates around the circumference of the original circle? Will the ratio of the radii make a difference? Will it make a difference if the circle is tangent on the interior or the exterior? The answer to all of these questions is yes.
First, let us look at a few examples of tangent circles with 1-nth of the radius of the original circles. We will use these to find a pattern and make a conjecture as to the number of revolutions the tangent circles will make. Click on the links below to open GSP sketches of the given description. Then, click on the animate buttons and count the revolutions.
Tangent Circles with a radius one-nth of the original
a) one-half
b) one-third
c) one-fourth
Did you count the revolutions correctly? Click on the answers to check your counts. Now, do you have a conjecture as to the rule for the number of revolutions any circle will make?
Now that you think you have a rule, try these tangent circles that are still proportional but not 1-nth of the radius of the original circle.
Tangent Circles other than one-nth of the original
a) two-thirds
Did your conjecture hold for these scenarios? Do you need to modify your conjecture?
Finally, it is time to prove a rule for the number of revolutions the tangent circle will make. Click here for the proofs.